Begin'R
Les statistiques avec R
Navigation
[Retour au sommaire]
# Graphiques en 3D :Objectifs Réaliser des **nuages de points** et des **surfaces de réponse** en **3D statiques** Les commandes sont présentées sur le jeu de données **Melons.csv** et les exercices proposés portent sur le jeu de données **Her.csv**. :Remarque : Besoin de quelques rappels pour l'importation et la préparation du jeu de données ? {#rq_preparation_donnees_graphiques_de_base, toggle=collapse, title-display=show} Le jeu de données **Melons** est issu d'une étude réelle relative à un essai variétal sur des melons. Elle a pour objectif de repérer les facteurs influençant le calibre des melons. Le jeu de données **Her**, issu d'une étude réelle sur des patients, présente les caractéristiques du corps humain : la taille et la masse corporelle, l'indice de masse corporelle, le pouls, la tension diastolique et systolique, les dimensions de différents organes en fonction du sexe et de l'âge. Les liens ci-dessous permettent de télécharger les fichiers de données, de visionner une vidéo expliquant la description associée et d'obtenir les lignes de code pour importer le jeu de données sur R. | Jeu de données | Excel | CSV | Présentation | Commande R | Explication | |-----------------|--------|-------------|----------------|------------|-------------| | Données Melons | [](donnees/DonneesMelons.xlsx) | [](donnees/DonneesMelons.csv) | [](video/DonneesMelons.html) | [Lignes de code pour importer et préparer le jeu de données](#ligne_code_importation) | [Explications sur la préparation du jeu de données](#explication_preparation_importation) | | Données Her | | [](donnees/DonneesHer.csv) | | [Lignes de code pour importer et préparer le jeu de données](#ligne_code_importation2) | [Explications sur la préparation du jeu de données](#explication_preparation_importation2) | :Exemple {#ligne_code_importation, toggle=popup} ```r Melons <- read.csv2("DonneesMelons.csv", header = TRUE, stringsAsFactors = TRUE) Melons <- transform(Melons, Creneau = as.ordered(Creneau), Couverture = as.factor(Couverture)) quatre_melons <- subset(Melons, Variete=='Cezanne'|Variete=='Fidji'|Variete=='Hugo'|Variete=='Manta') quatre_melons$Variete <- droplevels(quatre_melons$Variete) ``` :Exemple {#explication_preparation_importation, toggle=popup} Dans un premier temps, [importer le jeu de données melons sur RStudio](caps_2_3_importation_CSV.html). ```r Melons <- read.csv2("DonneesMelons.csv", header = TRUE, stringsAsFactors = TRUE) Melons <- transform(Melons, Creneau = as.ordered(Creneau), Couverture = as.factor(Couverture)) ``` Les valeurs manquantes sont supprimées du tableau de données avec la fonction **`na.omit()`**: ```r DonneesMelons<-na.omit(Melons) ``` Seules les variables `Duree`, `K` et `Poids` sont considérées par la suite. Pour cela, l'extraction peut être effectuée à l'aide de la commande **`subset()`** dans un objet nommé `melons`. Cette commande quand elle est appliquée à un jeu de données a l'avantage de retourner un **objet de la classe `data.frame`**. ```r melons<-subset(DonneesMelons, select = c(Duree,K, Poids)) ``` :Exemple {#ligne_code_importation2, toggle=popup} ```r her=read.csv2("donnees/DonneesHer.csv", header = TRUE, stringsAsFactors = TRUE) sante=subset(her,select=c(POIDS,TAILLE,BRAS)) ``` :Exemple {#explication_preparation_importation2, toggle=popup} Dans un premier temps, importer le jeu de données Her sur RStudio : ```r her <- read.csv2("donnees/DonneesHer.csv", header = TRUE, stringsAsFactors = TRUE) ``` Dans un second temps, sélectionner les variables d'intérêt POIDS, TAILLE et BRAS : ```r sante=subset(her,select=c(POIDS,TAILLE,BRAS)) ``` ### Introduction {#bloc_intro} + Un **nuage de points en 3D** est une représentation 3D d'un ensemble de N triplets $\{x_{i},y_{i},z_{i}\}$, avec i= 1 à n + Une **surface de réponse en 3D** est une représentation d'une fonction $f(x,y) : \mathbb{R}^{2}\to \mathbb{R}$ ### Réaliser les graphiques 3D statiques | Rôle | Commande R | Package |Exemple |Exercice| |:---------------------:|:--------------------:|:--------------------:|:--------------------:|:---------------------:| |Nuage de points statique | `scatterplot3d()` | **`scatterplot3d`** | [ici](#exemple_nuage_stat)| [ici](#exo_nuage_stat) | |Surface de réponse | `persp()` | **`scatterplot3d`** | [ici](#exemple_surf_stat)| [ici](#exo_surf_stat)| :Exemple {#exemple_nuage_stat, toggle=popup} Ici, la commande `scatterplot3d()`, qui est dans le package du même nom, est employée. Cette commande a au minimum un argument qui est le tableau de données (obligatoirement un data frame) regroupant les données des **3 variables** que vous voulez visualiser en 3D avec d'abord, la variable sur l'axe horizontal (x), puis celle sur l'axe de la profondeur (y) et enfin celle en ordonnées (z). L'objet `melons` est l'argument de la commande `scatterplot3d()` qui réalise le nuage de points. ```r library(scatterplot3d) ``` ```r nuage3d=scatterplot3d(melons) ``` 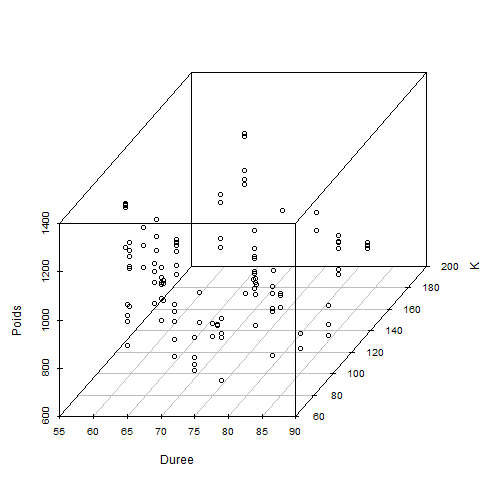 :Remarque importante {#rq_nuage3D, toggle=collapse} + Attention, sur l'axe vertical on a z et non y: c'est contre-intuitif. + La commande de R `data.frame()` crée des tableaux de données de la classe data frame. :Exemple {#exemple_surf_stat, toggle=popup} Pour faire un graphique 3D de la fonction $Z= f(X,Y)$, la commande `persp()` est employée. Elle est intéressante car dans la majorité des cas, les valeurs de $x$ et de $y$ sont des séquences de nombres. Il est supposé que vous savez créer votre propre [commande](caps_algo_6_fonctions.html) de R via la commande `function()`. Voici les **cinq étapes** pour faire le graphique : 1. Créer x qui doit être une séquence de nombre 2. Créer y qui doit être une séquence de nombre 3. Créer votre commande avec `function()` 4. Créer un objet z qui est une matrice contenant les valeurs de votre commande pour tous les couples (x,y) possibles avec `outer()` 5. Utiliser `persp()`qui a comme arguments x, y et z. La **fonction** est : $z=\displaystyle x\times exp(-(x^{2})-(y^{2}))$ Le **graphique de z** est réalisé pour 100 valeurs de x et de y comprises entre -2 et 2. ```r x<-seq(-2,2,length.out=100) y<-seq(-2,2,length.out=100) votrefonction<- function(x, y){x*exp(-(x^2)-(y^2))} z<-outer(x,y,votrefonction) persp(x,y,z) ``` 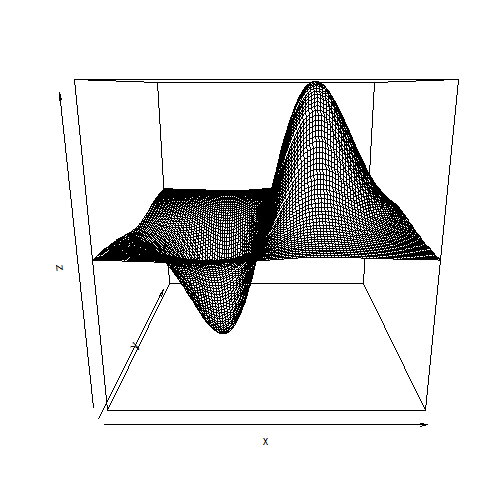 :Remarque {#rq_persp, toggle=collapse} La commande `persp()`nécessite des **séquences de nombres** ou des **matrices**. Dans le cas de data frames, Il sera donc nécessaire de les transformer en séquence. :Exercice : Réaliser un nuage de points en 3D {#exo_nuage_stat, toggle=popup} A partir du jeu de données Her.csv, créez l'objet `sante` qui contient les variables `POIDS`, `TAILLE` et `BRAS` dans cet ordre en utilisant la commande `subset()`, puis réalisez un nuage de points en 3D avec ces 3 variables en utilisant la commande `scatterplot3d()`. :Corrigé {#corr_exo_nuage_stat, toggle=collapse} ```r library(scatterplot3d) her=read.csv2("donnees/DonneesHer.csv", header = TRUE, stringsAsFactors = TRUE) sante=subset(her,select=c(POIDS,TAILLE,BRAS)) nuage3Dnew=scatterplot3d(sante) ``` 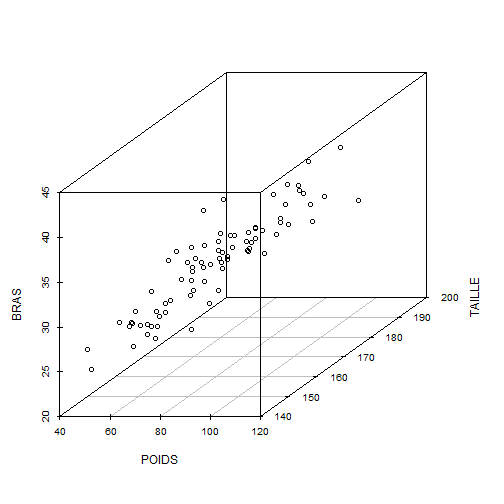 :Exercice : Réaliser une surface de réponse en 3D {#exo_surf_stat, toggle=popup} Réaliser un graphique en 3D de la fonction $w=\displaystyle \frac{sinus(u^2+v^2)}{\mid (u*v)\mid+1}$ pour 100 valeurs de u et de v comprises entre -2.5 et 2.5. :Corrigé {#corr_exo_surf_stat, toggle=collapse} ```r u<-seq(-2.5,2.5,length.out=100) v<-seq(-2.5,2.5,length.out=100) nouvellefonction<- function(u, v){ sin(u^2+v^2)/(abs(u*v)+1)} w<-outer(u,v,nouvellefonction) persp(u,v,w) ``` 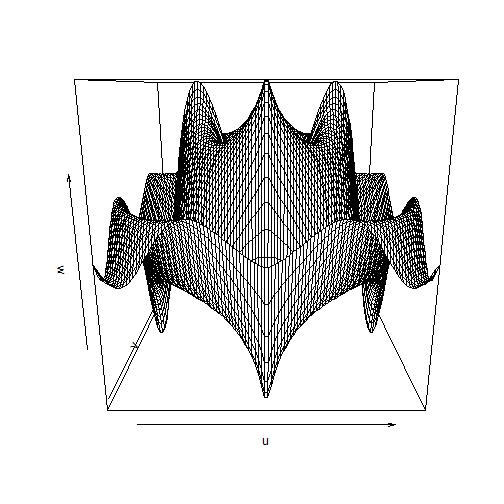 :Suite Graphiques 3D {#3D, toggle=collapse, title-display=hidden} [Graphiques 3D statiques](caps_10_1_graphiques_3d_statique.html) [Graphiques 3D dynamiques](caps_10_2_graphiques_3d_dynamique.html)