Begin'R
Les statistiques avec R
Navigation
[Retour au sommaire]
## Analyse qualitative des plans d'expériences : Graphiques des effets {#quali} :Objectifs Interpréter qualitativement un plan d'expériences via le tracé des graphiques des effet des facteurs et des interactions La représentation graphique de l'évolution d'une réponse avec le niveau des facteurs constitue une première approche instructive de l'influence des différents facteurs. ### Graphiques des effets des facteurs `MEPlot()` La commande `MEPlot()` du package FrF2 permet de tracer les graphiques des effets de tous les facteurs étudiés sur une réponse grâce à une seule ligne de commande. | **Argument** | **Rôle** | **Exemple**| |-------------|-----------|-----------| |obj|Nom de l'objet contenant le plan d’expériences et les réponses|[ici](#grapheff)| |response| Chaîne de caractères correspondant au nom d’une des réponses, par défaut la première réponse de la liste|| : Rappel générer le plan 2 {#gene, toggle=collapse} ```r plan2<-FrF2(nruns=8, nfactors=3, factor.names=c("temps", "temperature","agitation"), randomize=FALSE, replications=2) ``` ``` ## creating full factorial with 8 runs ... ``` ```r plan2<-add.response(plan2, response="donnees/2-3.csv", InDec=",") ``` :Exemple{#grapheff, toggle=popup} Le graphique des effets des facteurs étudiés dans le plan d'expériences plan2 sur la réponse y2 est donné par la commande : ```r MEPlot(plan2, response="y2") ``` 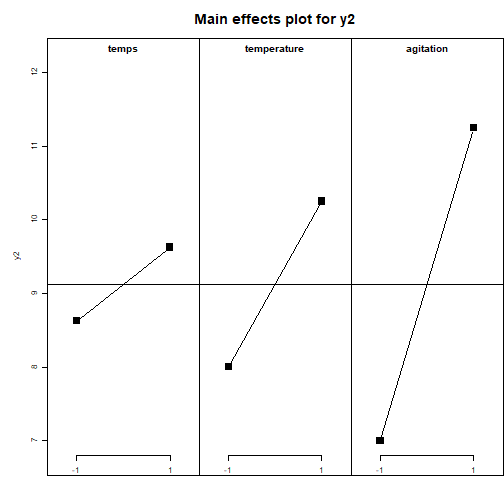 :Compléments : Interprétration du graphique des effets des facteurs {#cpltinteff, toggle=collapse} L'interprétation des **graphiques des effets des facteurs** repose sur l'analyse de la pente de la droite obtenue. Plus la droite a une pente importante (négative ou positive), plus l'effet du facteur sur la réponse est marqué. Afin de comparer facilement les graphiques des effets de différents facteurs sur une même réponse, il est important d'utiliser la même échelle pour l'axe des ordonnées sur les différents graphiques. Ici, dans l'exemple du plan 2, l'agitation est le facteur le plus influent. La modification du niveau de ce facteur du niveau -1 au niveau +1 provoque une augmentation de la réponse de ~4 unités (passage de y2 de 7 à 11) ### Graphiques des effets des interactions `IAPLot()` La commande `IAPlot()` du package FrF2 permet de tracer les graphiques des effets des interactions pour une réponse. Toutes les interactions de premier ordre entre les facteurs (c'est à dire les interactions des facteurs 2 à 2) sont représentées grâce à une seule ligne de commande. | **Argument** | **Rôle** | **Exemple**| |-------------|-----------|-----------| |obj|Nom de l'objet contenant le plan d’expériences et les réponses| |response| Chaîne de caractères correspondant au nom d’une des réponses, par défaut la première réponse de la liste|[ici](#graphit)| |show.alias| Si = TRUE, cela fait apparaître sur les graphiques le numéro de l'alias contenant l'interaction considérée|[ici](#numaliase)| |select|Sélectionne les interactions à représenter|[ici](#select)| :Aide{#numaliase, toggle=popup, title-display=hidden} Sur le graphique des interactions, plusieurs "cases" ayant le même numéro représentent donc la même interaction. Les graphiques contenus dans des cases de même numéro peuvent présenter une allure différente liée au choix du facteur porté en abscisse. :Aide{#select, toggle=popup, title-display=hidden} le code suivant donne l'interaction température - agitation sur la réponse y1 du plan2 ```r IAPlot(plan2, response="y1", show.alias=TRUE, select=c(2,3)) ``` 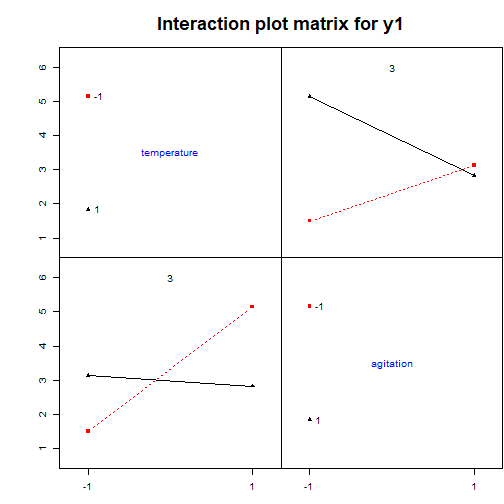 :Exemple{#graphit, toggle=popup, title-display=hidden} Le graphique des effets des interactions pour la réponse y1 du plan2 est donné par la commande `IAPLot()`. ```r IAPlot(plan2, response="y1", show.alias=TRUE) ``` 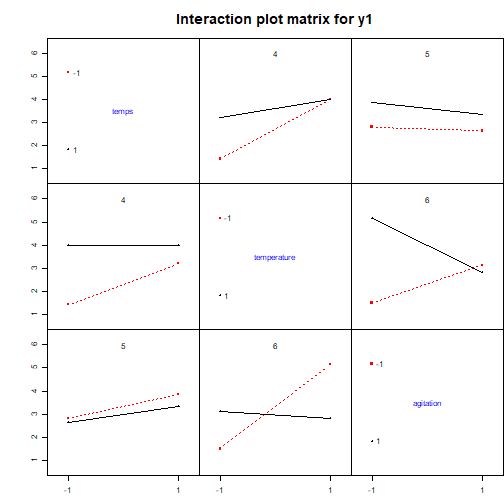 Sur cet ensemble de graphiques, on trouve à l'intersection d'une ligne et d'une colonne le graphique correspondant à l'interaction du facteur dont on trouve le nom sur la colonne et de celui que l'on trouve sur la ligne. Sur ces graphiques, le facteur dont le niveau varie de -1 à +1 sur chaque courbe est celui que l'on trouve dans la colonne, tandis que le facteur explicatif correspondant au facteur prenant le niveau -1 sur la courbe rouge et +1 sur la courbe noire, est le facteur que l'on trouve sur la ligne. Ici, le graphique numéroté 4 dans la première colonne présente le graphique de l'interaction temps-température. Sur ce graphique la courbe en trait plein noir présente l'évolution de la réponse y1 en fonction du niveau du facteur temps lorsque la température est au niveau +1. La courbe en trait pointillé rouge présente l'évolution de la réponse y1 en fonction du niveau du facteur temps lorsque la température est au niveau -1. Sur le second graphique numéroté 4 situé sur la première ligne du tableau, c'est la température qui varie du niveau -1 au niveau +1, tandis que le temps est au niveau +1 pour la courbe noire et au niveau -1 pour la courbe rouge. L'ensemble des arguments habituels des commandes graphiques peut également être utilisé avec les commandes `MEPlot()` et `IAPlot()`. Ces commandes ne fonctionnent pas avec tous les types de plan d'expériences, notamment elles ne sont pas utilisables lorsque le plan comprend des points au centre. :Compléments : Interprétation des graphiques des effets des interactions {#cpltitit, toggle=collapse} L'interprétation des **graphiques des effets des interactions** repose sur l'analyse du parallélisme des droites. Deux droites parallèles signent une absence d'interaction (la réponse augmente ou diminue en fonction du facteur représenté en abscisse indépendamment du niveau du second facteur). A l'inverse deux droites non parallèles indiquent une interaction "forte" entre les deux facteurs représentés. Ainsi dans l'exemple de la réponse y1 pour le plan2 : a. Il n'y a pas ou peu d'interaction entre l'agitation et le temps. En effet, les droites de l'interaction 5 sont quasiment parallèles. Augmenter l'agitation du niveau -1 à +1, lorsque le temps est au niveau -1, ne provoque quasiment pas de modification de la réponse (y1~2,7). Lorsque le temps est au niveau +1, cette même modification de l'agitation provoque une légère diminution de y1 (passage de ~3,8 à ~3,5). b. Il existe une interaction forte entre température et agitation. En effet, les droites de l'interaction 6 ont des pentes très différentes. Augmenter l'agitation du niveau -1 à +1, lorsque la température est au niveau -1, provoque une augmentation de y1 de ~1,5 à 3. Lorsque la température est au niveau +1, cette même modification de l'agitation provoque une diminution de y1 de ~5,5 à 3. Donc, le niveau pris par la température modifie la variation de y1 en fonction de l'agitation. :Compléments : Que faire si les commandes `IAPlot()` et `MEPlot()` ne fonctionnent pas ?{#cpltgraph, toggle=collapse} Si le plan d'expériences n'est pas dans le bon format ou s'il comprend des points au centre, les commandes `IAPlot()` et `MEPlot()` ne peuvent pas être utilisées. Dans ce cas là, il faut trouver des voies alternatives et souvent moins pratiques pour tracer les graphiques des effets. Parmi ces méthodes, on trouvera l'emploi de la commande `interaction.plot()` ou encore la méthode "manuelle" consistant à calculer les moyennes conditionnelles des réponses. * **Utilisation de `interaction.plot()`** |Commande R|Avantage|Inconvénient|Exemple| |-------|--------|------------|-------| |interaction.plot(facteur 1, facteur 2, réponse)|Syntaxe facile|Ne permet de tracer que les graphiques des effets des interactions et ne fonctionne pas pour les points au centre|[ici](#itplot)| :Exemple {#itplot, toggle=popup} Pour l'interaction température / agitation du plan2 sur la réponse y1 : ```r interaction.plot(plan2$agitation, plan2$temperature, plan2$y1) ``` 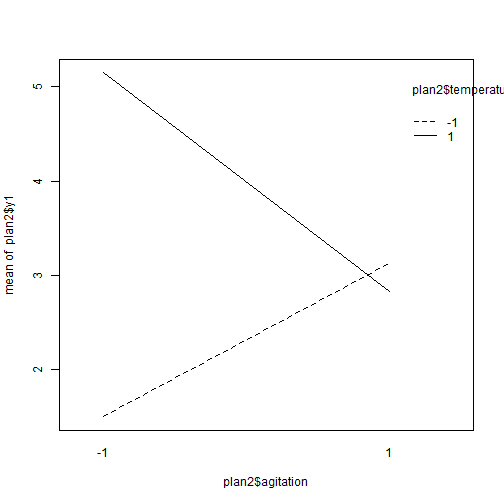 On peut améliorer la présentation du graphique grâce aux options graphiques classiques : ```r interaction.plot(plan2$agitation, plan2$temperature, plan2$y1, xlab="Agitation", ylab="y1", trace.label ="Température", col=c("blue", "red")) ``` 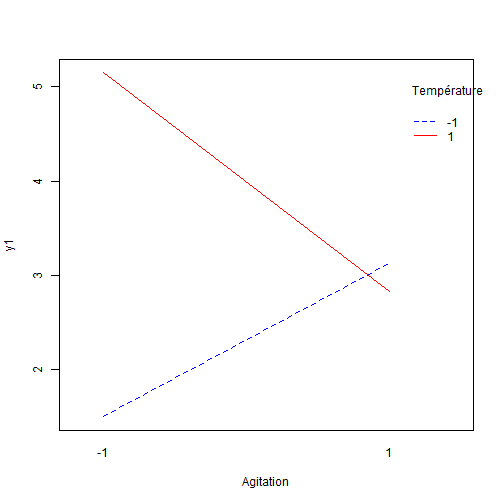 * **Méthode manuelle** |Commande R|Avantage|Inconvénient|Exemple| |-------|--------|------------|-------| |plot|On peut faire ce que l'on veut|Peut être long et fastidieux|[ici](#itplotman)| :Exemple{#itplotman, toggle=popup, display-title=hidden} Ici, le tracé des graphiques se fait complétement manuellement. Les graphiques des effets présentent l'évolution de la réponse en fonction des niveaux de un ou deux facteurs (l'un représenté en abscisse et le second, pour les graphiques des effets des interactions, en légende). Pour les tracer, il faut tout d'abord calculer la moyenne de la réponse pour chaque niveau de facteur (graphiques des effets des facteurs) ou pour chaque combinaison de niveaux des facteurs (graphiques des effets des interactions). 1. Calculer les moyennes conditionnelles avec la commande `aggregate(réponse~facteur A, data=plan, mean)` pour un seul facteur, ou `aggregate(réponse~facteur A + facteur B, data=plan, mean)` pour une interaction. Mettre le résultat dans un objet à l'aide de l'affectation <- 2. Tracer le graphique des effets des facteurs à l'aide la commande `plot(nom de l'objet contenant le résultat de aggregate)` 3. Tracer le graphique des effets des interactions. Sélectionner les données dans le résultat de aggregate tel que l'un des deux facteurs soit égal à -1 (sub<-subset(résultat de aggregate, facteur1==-1)) puis tracer à l'aide de la commande `plot(sub$réponse~sub$facteur 2)`. Faire de même avec facteur1=1 et tracer sur le graphique pré-existant). | Effet d'un facteur | Effet d'une interaction |Effet d'un facteur avec points au centre| |:-------------:|:-----------:|:-----------:| |[ici](#plotmeanseff2)|[ici](#plotmeansit2)|[ici](#plotmeanscentre)| :Exemple {#plotmeanseff2, toggle=popup, display-title=hidden} Graphique de l'effet du facteur agitation sur y1 dans le plan d'expériences plan2 ```r ef1<-aggregate(y1~agitation, data=plan2, mean) ef1 ``` ``` ## agitation y1 ## 1 -1 3.325 ## 2 1 2.975 ``` ```r agitation<-c(-1,1) # définition des bornes à mettre en abscisse plot(ef1$y1~agitation, type="b", ylab="y1", xlab="Agitation") ``` 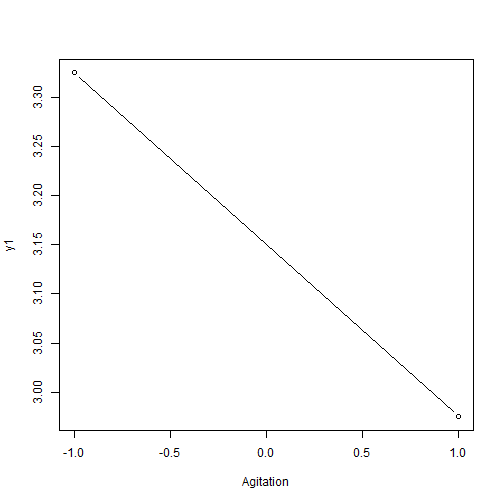 :Exemple {#plotmeansit2, toggle=popup, display-title=hidden} Graphique de l'effet de l'interaction agitation-température sur y1 dans le plan d'expériences plan2. ```r ef2<-aggregate(y1~agitation+temperature, data=plan2, mean) sub1<-subset(ef2, agitation==-1) sub2<-subset(ef2, agitation==1) temperature<-c(-1,1) plot(sub1$y1~temperature, ylab="y1", col="blue", type="b") lines(sub2$y1~temperature, ylab="y1", col="red", type="b") legend("topleft", legend=c("-1", "+1"), lty=c(1,1),col=c("blue","red"),title=c("agitation"),bty='n') ``` 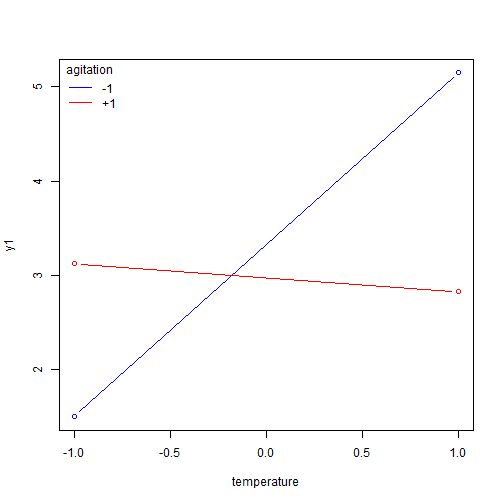 :Exemple {#plotmeanscentre, toggle=popup, display-title=hidden} :Générer un plan avec points au centre {#gene2, toggle=collapse} Pour générer un plan factoriel complet non randomisé de type $2^{3}$ avec 3 points au centre et y ajouter la réponse contenue dans le fichier 2-3-0.csv [](donnees/2-3-0.csv) ```r plan3<-FrF2(nruns=8, nfactors=3, randomize=FALSE, ncenter=3) ``` ``` ## creating full factorial with 8 runs ... ``` ```r plan3<-add.response(plan3, "donnees/2-3-0.csv", InDec=",") ``` Graphique de l'effet des facteurs sur y1 dans le plan d'expériences plan3 ```r ef1<-aggregate(y1~A, data=plan3, mean) ef2<-aggregate(y1~B, data=plan3, mean) ef3<-aggregate(y1~C, data=plan3, mean) x<-c(-1,0,1) # définition des bornes à mettre en abscisse par(mfrow=c(1,3)) plot(ef1$y1~x, type="b", ylab="y1", xlab="A", ylim=c(2,3)) plot(ef2$y1~x, type="b", ylab="y1", xlab="B", ylim=c(2,3)) plot(ef1$y1~x, type="b", ylab="y1", xlab="C", ylim=c(2,3)) ``` 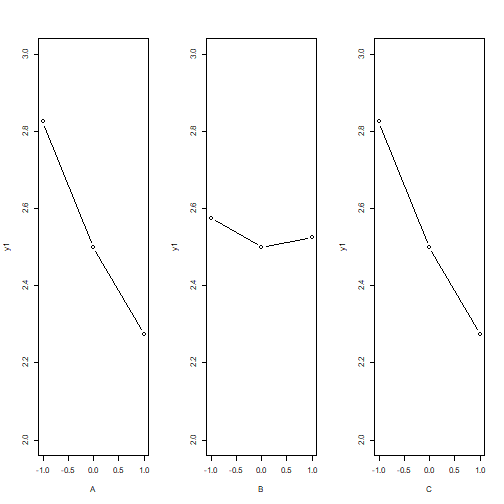 :Compléments faire un graphique plus esthétique {#cpltcentre, toggle=collapse} Un graphique des effets avec points au centre sera plus facile à interpréter en traçant une ligne rejoignant les moyennes aux niveaux -1 et +1 (points du cube) puis en ajoutant la moyenne des points au centre. Ce cette façon, il est plus aisé de vérifier que le point au niveau 0 s'aligne bien avec la droite des effets -1/+1. Pour se faire, il faut calculer séparément la moyenne des points au centre et les moyennes aux niveaux -1/+1. La commande `subset()`peut permettre de faire cette sélection en regardant si le niveau d'un facteur est nul ou non. On récupère une partie du plan contenant les points du cube (lorsque le niveau du facteur est différent de 0 (condition `plan$facteur1!=0` sur R)) et une partie contenant les points au centre (lorsque le niveau du facteur est égal à 0 (condition `plan$facteur1==0` sur R)) * Pour avoir les points au centre : plan_centre<-subset(plan, plan$facteur1==0)) * Pour avoir les points du cube plan_cube<-subset(plan, plan$facteur1!=0)) L'utilisation de la commande `subset()` donne des objets qui ne sont plus de type class design, donc certaines fonctionnalités liées aux plans d'expériences ne fonctionnent pas sur ces objets. :Exemple {#excentre, toggle=collapse} Le graphique de l'effet du facteur A sur la réponse y1 dans le plan3 : ```r cube<-subset(plan3, plan3$A!=0) centre<-subset(plan3, plan3$A==0) ef1<-aggregate(y1~A, data=cube, mean) A<-c(-1, 1) plot(ef1$y1~A, type="b", ylab="y1", xlab="A", ylim=c(2,3)) points(0, mean(centre$y1)) ``` 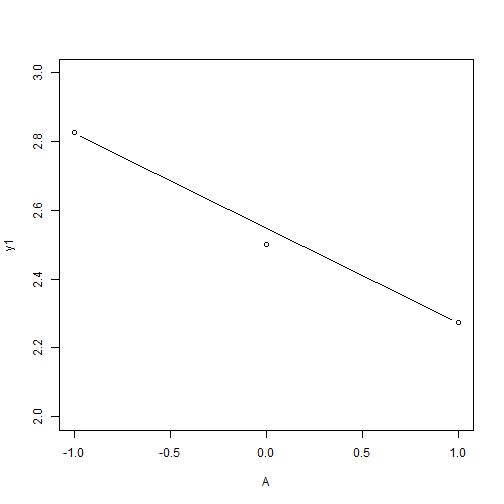 :Suite Plans d'expériences {#plexp, toggle=collapse, title-display=hidden} [Générer un plan d'ordre 1](caps_11_1_generer_un_plan_ordre_1.html) [Générer un plan d'ordre 2](caps_11_2_generer_un_plan_ordre_2.html) [Ajouter les réponses](caps_11_3_plans_experiences_ajout_reponse.html) [Analyse qualitative : graphiques des effets](caps_11_4_plans_experiences_graphiques_effets.html) [Analyse quantitative : régression et ANOVA](caps_11_5_plans_experiences_regression_anova.html) [Plans factoriels fractionnaires : interprétation et plans complémentaires](caps_11_6_plans_experiences_interpretation_fractionnaire_complementaire.html) [Isoréponses](caps_11_7_plans_experiences_isoreponses.html) [Exercices bilan](caps_11_8_exercice_recap_plans_exp.html)