Begin'R
Les statistiques avec R
Navigation
[Retour au sommaire]
## Analyse quantitative des plans d'expériences : Régression et ANOVA {#quanti} :Objectifs * Réaliser une régression multilinéaire sur un plan d'expériences * Identifier les effets significatifs via une ANOVA ### Régression multilinéaire La régression multi-linéaire permettant de déterminer le modèle associé à un plan d'expériences peut être réalisée simplement à l'aide de la commande `lm()`; d'autres commandes permettent de réaliser cette étape avec une syntaxe de l'équation du modèle plus simple. La syntaxe générale de la commande est : `lm(réponse~modèle, data=plan)`. La particularité des plans d'expériences est la nécessité de faire apparaître des termes d'interaction dans les modèles. Un terme d'interaction dans un modèle s'écrit A:B:C par exemple pour l'interaction triple entre les facteurs A, B et C. :Compléments : Autres écritures des modèles possibles {#modele, toggle=collapse} Le tableau suivant présente le type de modèle associé à chaque type de plan d'expériences (présenté pour un plan à trois facteurs) ainsi que la syntaxe du modèle. | Modèle | Type de plan associé |Fonction de régression|Syntaxe du modèle| |-------------|-----------|-------------|-----------| |facteurs + **toutes** les interactions|plan d'ordre 1 (factoriel complet ou fractionnaire)|`lm()`|y~A+B+C+A:B+A:C+B:C+A:B:C| | ||`lm()`|y~A`*`B`*`C| |||`lm()`|y~(A+B+C)^3| |facteurs + **interactions d'ordre i**|plan d'ordre 1| `lm()`| y~(A+B+C)^i| |facteurs + toutes les interactions + **efffets quadratiques**|plan ordre 2 (composite centré ou Box-Behnken)|`lm()`|y~A+B+C+A:B+A:C+B:C+A:B:C+I(A`^`2)+I(B`^`2)+I(C`^`2)| |||`lm()`|y~A`*`B`*`C+I(A`^`2)+I(B`^`2)+I(C`^`2)| |facteurs + **interactions d'ordre 1** + effets quadratiques||`rsm()` (package rsm)|y~SO(A,B,C)| :Exemple de régression {#reg, toggle=collapse} :Rappel : Générer le plan d'expériences plan2 {#gene, toggle=collapse} ```r library(FrF2) ``` ```r plan2<-FrF2(nruns=8, nfactors=3, factor.names=c("temps", "temperature","agitation"), randomize=FALSE, replications=2) ``` ``` ## creating full factorial with 8 runs ... ``` ```r plan2<-add.response(plan2, response="donnees/2-3.csv", InDec=",") ``` Le code suivant permet d'avoir la régression multi-linéaire donnant l'effet de tous les facteurs et de toutes les interactions sur la réponse y1 du plan d'expériences plan2. ```r regressiony1<-lm(y1~temps+temperature+agitation +temps:temperature+temps:agitation+temperature:agitation +temps:temperature:agitation, data=plan2) ``` Le code suivant est équivalent : ```r regressiony1<-lm(y1~temps*temperature*agitation, data=plan2) ``` ### ANOVA #### Vérifier les hypothèses Une ANOVA réalisée sur les résultats de la régression permet de conclure sur la significativité des effets. Avant d'interpréter les résultats de l'ANOVA, il faut vérifier que les hypothèses associées sont bien validées. Cette vérification peut se faire graphiquement ou via des tests statistiques. Ces différentes méthodes sont répertoriées dans le tableau ci-dessous |Rôle|Hypothèse testée|Commande R|Exemple|Remarque| |-------|----------------|----|--------|--------------| |Graphique|Homoscédasiticité|`plot()` avec l'objet contenant les résultats de la régression|[ici](#ploty1)|[ici](#gr1plexp)| |Graphique|Normalité des résidus|`plot()` avec l'objet contenant les résultats de la régression|[ici](#ploty1_2)|[ici](#gr2plexp)| |Test|Homoscédasticité|`ncvTest()` package car|[ici](#ncv)|Si p>0.05, l'hypothèse est validée au seuil de 95%| |Test|Normalité des résidus|`shapiro.test()`|[ici](#shapiro)|Si p>0.05, l'hypothèse est validée au seuil de 95%| :Exemple {#ploty1, toggle=popup, title-display= hidden} ```r plot(regressiony1) ```  :Exemple {#ploty1_2, toggle=popup, title-display= hidden} ```r plot(regressiony1) ``` 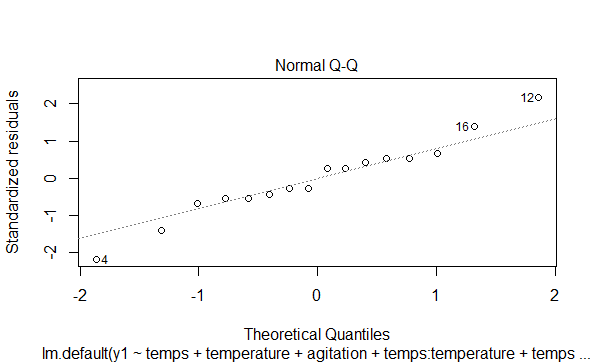 :Remarque {#gr1plexp, toggle=popup, title-display= hidden} Le graphique des résidus en fonction des valeurs prédites. Ce graphique ne doit pas présenter de schéma particulier (courbe en cloche [ordre du modèle non adapté] ou de répartition en entonnoir [hétéroscédasticité]). Sur ce graphique, les observations "aberrantes" (outliers) apparaissent avec leur numéro pour permettre de les retrouver; :Remarque {#gr2plexp, toggle=popup, title-display= hidden} Graphique de normalité des résidus : Les points doivent s'aligner sur la droite pour justifier de la distribution normale des résidus; :Exemple {#shapiro, toggle=popup, title-display= hidden} ```r shapiro.test(resid(regressiony1)) ``` ``` ## ## Shapiro-Wilk normality test ## ## data: resid(regressiony1) ## W = 0.97155, p-value = 0.8631 ``` :Exemple {#ncv, toggle=popup, title-display= hidden} ```r library(car) ``` ```r ncvTest(regressiony1) ``` ``` ## Non-constant Variance Score Test ## Variance formula: ~ fitted.values ## Chisquare = 5.938531, Df = 1, p = 0.014813 ``` :Remarque : Autres graphiques de diagnostic {#plotreg, toggle=collapse} Deux autres graphiques apparaissent lors de l'utilisation de la commande `plot()` avec l'objet contenant les résultats de la régression. 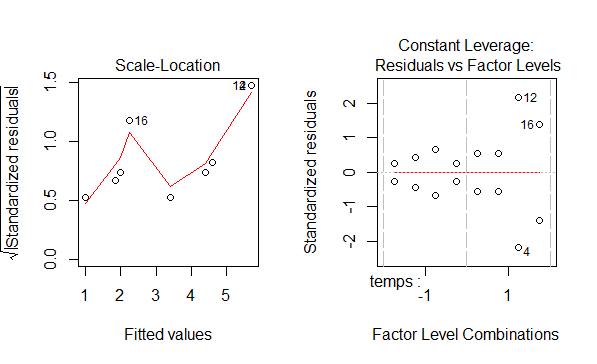 Le graphique de "scale location" est similaire au graphique des résidus et aucun schéma ne doit se distinguer pour pouvoir valider le modèle ; Le graphique des résidus en fonction des niveaux des facteurs. Ce graphique représente « le poids » de chaque expérience dans la régression. Les points éloignés du centroïde (point 0,0) ont une forte incidence sur la régression et leur suppression conduirait à largement modifier cette dernière. Ainsi les points situés au-delà des courbes en pointillé rouge sont des points à considérer car ils influent beaucoup sur la détermination du modèle. Ici, c'est l'effet de levier qui est mis en évidence. :Remarque Le cas représenté ici est un cas particulier puisque le graphique des résidus est symétrique par rapport à l'axe des abscisses. Ce cas particulier intervient dans le cas des plan répétés 2 fois (chaque expérience est faite en double) et ne constitue pas une raison pour rejeter les hypothèses liées à l'ANOVA. #### Réaliser l'ANOVA L'analyse de variance des résultats de la régression est faite avec la commande `anova()` avec l'objet contenant la régression. Les effets significatifs peuvent alors être identifiés. :Exemple : ANOVA sur la régression {#anova, toggle=collapse} ```r anova(regressiony1) ``` ``` ## Analysis of Variance Table ## ## Response: y1 ## Df Sum Sq Mean Sq F value Pr(>F) ## temps 1 3.063 3.0625 0.7014 0.42662 ## temperature 1 11.222 11.2225 2.5703 0.14756 ## agitation 1 0.490 0.4900 0.1122 0.74624 ## temps:temperature 1 3.240 3.2400 0.7421 0.41408 ## temps:agitation 1 0.123 0.1225 0.0281 0.87113 ## temperature:agitation 1 15.602 15.6025 3.5734 0.09537 . ## temps:temperature:agitation 1 3.610 3.6100 0.8268 0.38977 ## Residuals 8 34.930 4.3662 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ``` Interprétation : Au seuil de 95%, aucun facteur et aucune d'interaction n'a d'effet significatif sur la réponse y1. :Remarque : Nombre de paramètres et nombre d'expériences Le nombre de points expérimentaux disponibles doit être en adéquation avec le nombre de paramètres inclus dans le modèle. Il convient d'avoir au minimum une expérience de plus que le nombre de paramètres à déterminer afin d'avoir une évaluation de l'erreur expérimentale. Ainsi, avec un plan $2^3$ sans répétition et sans point au centre, vous ne pourrez évaluer statistiquement la significativité que de 7 paramètres (effets des facteurs $X_1, X_2, X_3$ et des interactions $X_1 X_2, X_1 X_3, X_2 X_3$ et la constante du modèle (moyenne des réponses)). L'interprétation des résultats de l'ANOVA doit se faire avec précaution, particulièrement pour les plans fractionnaires où le [désaliasage](caps_11_6_plans_experiences_interpretation_fractionnaire_complementaire.html) (définir quel effet aliasé dans un contraste significatif est significatif) reste manuel. :Suite Plans d'expériences {#plexp, toggle=collapse, title-display=hidden} [Générer un plan d'ordre 1](caps_11_1_generer_un_plan_ordre_1.html) [Générer un plan d'ordre 2](caps_11_2_generer_un_plan_ordre_2.html) [Ajouter les réponses](caps_11_3_plans_experiences_ajout_reponse.html) [Analyse qualitative : graphiques des effets](caps_11_4_plans_experiences_graphiques_effets.html) [Analyse quantitative : régression et ANOVA](caps_11_5_plans_experiences_regression_anova.html) [Plans factoriels fractionnaires : interprétation et plans complémentaires](caps_11_6_plans_experiences_interpretation_fractionnaire_complementaire.html) [Isoréponses](caps_11_7_plans_experiences_isoreponses.html) [Exercices bilan](caps_11_8_exercice_recap_plans_exp.html)