Begin'R
Les statistiques avec R
Navigation
[Retour au sommaire]
## Exercices récapitulatifs {#exrecap} :Objectifs Créer, interpréter et conclure sur une étude réalisée par plan d'expériences :Exercice plan factoriel complet {#exrecap, toggle=collapse} L'étude a pour but d'étudier, via un plan factoriel complet,3 facteurs susceptibles d'influer sur la texture de biscuits de type petits beurre: | Facteur | nom |domaine expérimental (niveaux -1/+1)| |-------------|-----------|-------------| | A| Température du four | 180°C à 220°C| | B| Temps de cuisson | 8 min à 16 min| |C| Épaisseur de la pâte |2 mm à 5mm| Les caractéristiques voulues pour ce plan sont : * Facteurs à 2 niveaux * Plan factoriel complet ($2^3$) * 3 répétitions de chaque expériences (répétitions groupées) * pas de randomisation Dans cet exercice il faut : 1. Créer le plan :Corrigé{#Q1, toggle=collapse} ```r library(FrF2) ``` ```r plan<-FrF2(nruns=8, nfactors=3, replications=3, repeat.only=TRUE, randomize=FALSE) ``` ``` ## creating full factorial with 8 runs ... ``` ```r plan ``` ``` ## run.no run.no.std.rp A B C ## 1 1 1.1 -1 -1 -1 ## 2 2 1.2 -1 -1 -1 ## 3 3 1.3 -1 -1 -1 ## 4 4 2.1 1 -1 -1 ## 5 5 2.2 1 -1 -1 ## 6 6 2.3 1 -1 -1 ## 7 7 3.1 -1 1 -1 ## 8 8 3.2 -1 1 -1 ## 9 9 3.3 -1 1 -1 ## 10 10 4.1 1 1 -1 ## 11 11 4.2 1 1 -1 ## 12 12 4.3 1 1 -1 ## 13 13 5.1 -1 -1 1 ## 14 14 5.2 -1 -1 1 ## 15 15 5.3 -1 -1 1 ## 16 16 6.1 1 -1 1 ## 17 17 6.2 1 -1 1 ## 18 18 6.3 1 -1 1 ## 19 19 7.1 -1 1 1 ## 20 20 7.2 -1 1 1 ## 21 21 7.3 -1 1 1 ## 22 22 8.1 1 1 1 ## 23 23 8.2 1 1 1 ## 24 24 8.3 1 1 1 ## class=design, type= full factorial ## NOTE: columns run.no and run.no.std.rp are annotation, ## not part of the data frame ``` 2. Ajouter la réponse contenue dans le fichier ex_recap_1.csv [](donnees/ex_recap_1.csv) :Corrigé {#Q2, toggle=collapse} ```r plan<-add.response(plan, "donnees/ex_recap_1.csv", InDec=",") ``` 3. Tracer les graphiques des effets des facteurs et des interactions :Corrigé {#Q3, toggle=collapse} ```r MEPlot(plan) ``` ``` ## analysing repeated measurement mean ``` 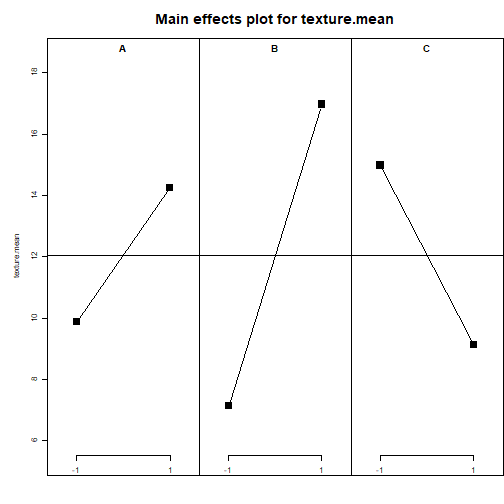 ```r IAPlot(plan) ``` ``` ## analysing repeated measurement mean ``` 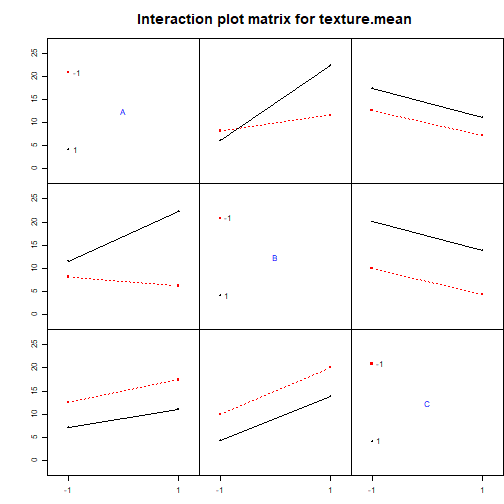 4. Identifier les effets significatifs :Aide{#sign, toggle=collapse} Pour identifier les effets significatifs, il faut : * Réaliser la régression * Vérifier les hypothèses de l'ANOVA * Identifier les facteurs significatifs :Corrigé {#Q4, toggle=collapse} Réaliser la régression ```r regression<-lm(texture~A*B*C, data=plan) ``` Vérifier les hypothèses de l'ANOVA ```r library(car) ``` ```r par(mfrow=c(2,2)) plot(regression) ``` 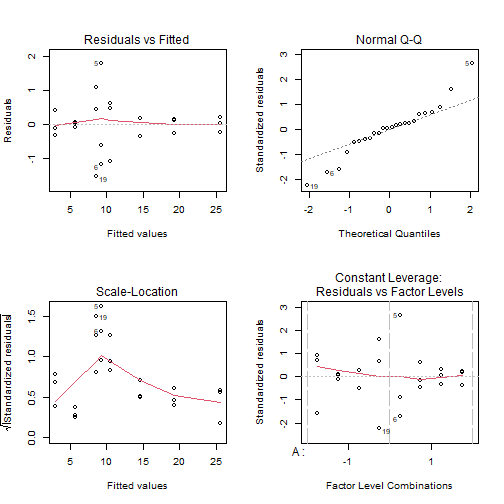 ```r ncvTest(regression) ``` ``` ## Non-constant Variance Score Test ## Variance formula: ~ fitted.values ## Chisquare = 1.770609, Df = 1, p = 0.18331 ``` ```r shapiro.test(resid(regression)) ``` ``` ## ## Shapiro-Wilk normality test ## ## data: resid(regression) ## W = 0.94731, p-value = 0.2368 ``` Identifier les facteurs significatifs ```r summary(regression) ``` ``` ## ## Call: ## lm.default(formula = texture ~ A * B * C, data = plan) ## ## Residuals: ## Min 1Q Median 3Q Max ## -1.51681 -0.26874 0.04663 0.26118 1.78803 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 12.0537 0.1692 71.237 < 2e-16 *** ## A1 2.1912 0.1692 12.950 6.77e-10 *** ## B1 4.9091 0.1692 29.012 2.90e-15 *** ## C1 -2.9230 0.1692 -17.275 9.04e-12 *** ## A1:B1 3.1923 0.1692 18.866 2.35e-12 *** ## A1:C1 -0.2215 0.1692 -1.309 0.209 ## B1:C1 -0.1558 0.1692 -0.921 0.371 ## A1:B1:C1 0.1392 0.1692 0.823 0.423 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.8289 on 16 degrees of freedom ## Multiple R-squared: 0.9905, Adjusted R-squared: 0.9863 ## F-statistic: 238.1 on 7 and 16 DF, p-value: 5.801e-15 ``` ```r step(regression) ``` ``` ## Start: AIC=-2.74 ## texture ~ A * B * C ## ## Df Sum of Sq RSS AIC ## - A:B:C 1 0.4652 11.459 -3.7419 ## <none> 10.994 -2.7365 ## ## Step: AIC=-3.74 ## texture ~ A + B + C + A:B + A:C + B:C ## ## Df Sum of Sq RSS AIC ## - B:C 1 0.582 12.042 -4.552 ## <none> 11.459 -3.742 ## - A:C 1 1.178 12.637 -3.394 ## - A:B 1 244.573 256.033 68.814 ## ## Step: AIC=-4.55 ## texture ~ A + B + C + A:B + A:C ## ## Df Sum of Sq RSS AIC ## <none> 12.042 -4.552 ## - A:C 1 1.178 13.219 -4.313 ## - A:B 1 244.573 256.615 66.869 ``` ``` ## ## Call: ## lm.default(formula = texture ~ A + B + C + A:B + A:C, data = plan) ## ## Coefficients: ## (Intercept) A1 B1 C1 A1:B1 A1:C1 ## 12.0537 2.1912 4.9091 -2.9230 3.1923 -0.2215 ``` :Compléments sur la fonction `step()`{toggle=collapse} La fonction `step()`permet de réduire le nombre de termes influents présents dans le modèle.Pour plus d'information sur [cette fonction](caps_9_3_regression_lineaire_multiple_affiner.html) :Suite Plans d'expériences {#plexp, toggle=collapse, title-display=hidden} [Générer un plan d'ordre 1](caps_11_1_generer_un_plan_ordre_1.html) [Générer un plan d'ordre 2](caps_11_2_generer_un_plan_ordre_2.html) [Ajouter les réponses](caps_11_3_plans_experiences_ajout_reponse.html) [Analyse qualitative : graphiques des effets](caps_11_4_plans_experiences_graphiques_effets.html) [Analyse quantitative : régression et ANOVA](caps_11_5_plans_experiences_regression_anova.html) [Plans factoriels fractionnaires : interprétation et plans complémentaires](caps_11_6_plans_experiences_interpretation_fractionnaire_complementaire.html) [Isoréponses](caps_11_7_plans_experiences_isoreponses.html) [Exercices bilan](caps_11_8_exercice_recap_plans_exp.html)