Begin'R
Les statistiques avec R
Navigation
[Retour au sommaire]
# ANOVA à un facteur : Réalisation et Vérification des hypothèses :Remarque : Besoin de quelques rappels pour l'importation et la préparation du jeu de données? {#rq_preparation_donnees_graphiques_de_base, toggle=collapse, title-display=show} Le jeu de données utilisé dans cette partie sur l'ANOVA est le jeu de données "Cépages". Ce jeu de données répertorie les pH de vins associés à trois cépages : Merlot, Cabernet Sauvignon (CS) et Cabernet Franc (CF). Le lien ci-dessous permet de télécharger le fichier de données et d'obtenir les lignes de code pour importer le jeu de données sur R. | Jeu de données | CSV | Commande R | |-----------------|-------------|------------| | Données Cépages | [](donnees/Cepages.csv) | [Importer le jeu de données](#ligne_code_importation_cepages) | :Exemple {#ligne_code_importation_cepages, toggle=popup} ```r donnees <- read.csv2("donnees/Cepages.csv", header = TRUE, stringsAsFactors = TRUE) ``` Il est vivement conseillé de vérifier que R a bien identifié la variable et le facteur. On peut utiliser : ```r str(donnees) ``` ``` ## 'data.frame': 15 obs. of 2 variables: ## $ Cepage: Factor w/ 3 levels "CF","CS","Merlot": 3 3 3 3 3 2 2 2 2 2 ... ## $ pH : num 3.32 3.15 3.19 3.24 3.3 3.53 3.63 3.54 3.57 3.6 ... ``` Des modifications peuvent être effectuées suivant les modalités présentées dans la partie [Manipulation de données](caps_2_7_corriger_type_variables.html). :Objectifs * Réaliser l'ANOVA * Vérifier les hypothèses de l'ANOVA Le traitement de données dans le cadre d'une ANOVA monofactorielle à effets fixés va être envisagé. Le modèle associé est $$Y_{ij} = \mu + \alpha_i + \varepsilon_{ij}$$ ## Réaliser l'ANOVA Le modèle est défini à l'aide de la fonction `aov()` en considérant les arguments : * formula = variable~facteur * data :Exemple{#ex1, toggle=collapse} Pour le jeu de données cépages: ```r modele = aov(formula = pH ~ Cepage, data = donnees) ``` ## Vérifier les hypothèses ### Graphiquement Les graphiques associés aux résidus pour vérifier que les distributions sont **homoscédastiques**, **indépendantes** et **gaussiennes** peuvent être obtenus par la commande `plot(aov(variable ~ facteur))`. Quatre graphiques sont alors affichés et apparaissent successivement en appuyant sur la touche Entrée. | Graphique | Description | Exemple| |-----------|-------------|--------| |n°1 (Residuals vs Fitted)|eprésentation des résidus en fonctions des moyennes (par niveau)|[ici](#plot1)| |n°2 (Normal Q-Q)| graphique quantile-quantile des résidus autour de la normalité| [ici](#plot2)| |n°3 (Scale-Location)| représentation des racines carrées des résidus “standardisés” en fonctions des moyennes (par niveau)| [ici](#plot3)| |n°4 (Constant Leverage ou Cook's distance)| graphique des résidus “standardisés” par niveau| [ici](#plot4)| :Exemple {#plot1, toggle=popup} ```r plot(modele,1) ``` 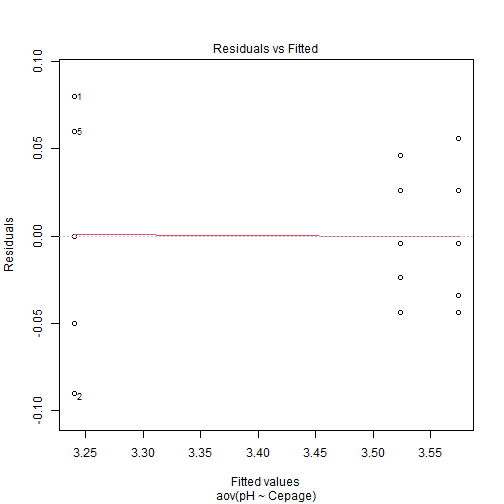 :Exemple {#plot2, toggle=popup} ```r plot(modele,2) ``` 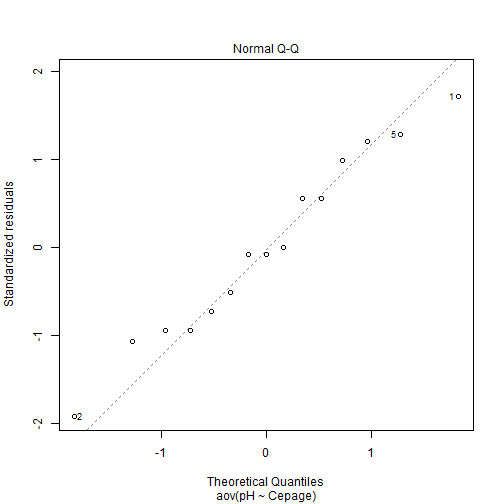 :Exemple {#plot3, toggle=popup} ```r plot(modele,3) ``` 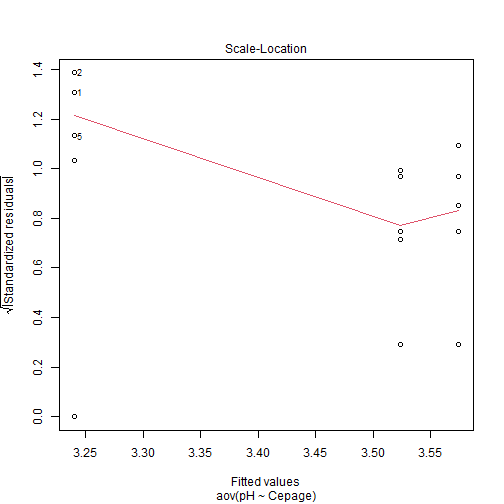 :Exemple {#plot4, toggle=popup} ```r plot(modele,4) ``` 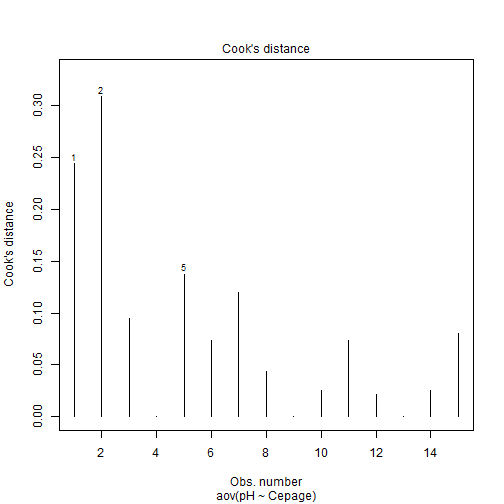 :Compléments afficher les 4 graphiques en 1 {#par, toggle=collapse} Pour davantage de lisibilité, on peut les afficher simultanément grâce à la commande par(mfrow=c(2,2)) ```r par(mfrow = c(2, 2)) plot(modele) ``` 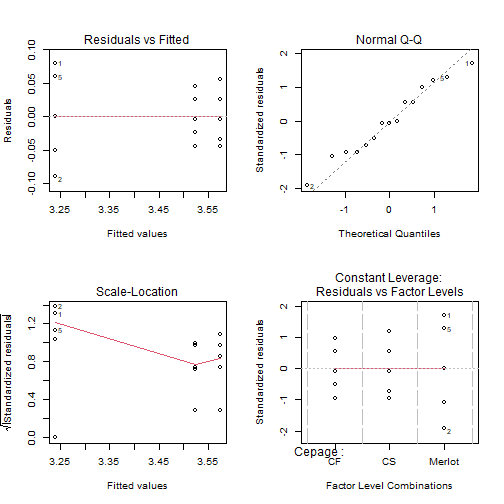 :Compléments sur les résidus {#residus, toggle=collapse} Les résidus standardisés sont obtenus en divisant les résidus de l'anova par $\sqrt{ \frac{SCE_{res}}{N} }$ où $N$ correspond au nombre (total) d'observations. On peut les obtenir soit par calcul, soit en utilisant la fonction `rstandard( )` appliquée au modèle. ```r # Détermination par calcul residus = resid(modele) # Détermination des résidus N=length(donnees$pH) SCE_res = sum(residus^2) # Détermination de la SCE résiduelle pouvant également être obtenue dans le tableau d'ANOVA (voir plus loin) round(residus / sqrt( (SCE_res/N) ),2) # Obtention des résidus standardisés arrondis aux centièmes. ``` ``` ## 1 2 3 4 5 6 7 8 9 10 11 12 13 ## 1.71 -1.92 -1.07 0.00 1.28 -0.94 1.20 -0.73 -0.09 0.56 -0.94 -0.51 -0.09 ## 14 15 ## 0.56 0.98 ``` ```r # Utilisation de la fonction `rstandard( ) ` res_standardises = rstandard(modele) round(res_standardises,2) ``` ``` ## 1 2 3 4 5 6 7 8 9 10 11 12 13 ## 1.71 -1.92 -1.07 0.00 1.28 -0.94 1.20 -0.73 -0.09 0.56 -0.94 -0.51 -0.09 ## 14 15 ## 0.56 0.98 ``` ### A l'aide de tests Des tests de normalité et d'homoscédasticité doivent porter sur les résidus liés à l’anova. Récupération des résidus Ils peuvent être obtenus en utilisant la fonction `resid()` voire `residuals()`. ```r residus=resid(modele) ``` Les fonctions permettant de tester la normalité et l'homodcédasticité des résidus sont : |Rôle| Commande R| Arguments|Exemple| |----|-----------|----------|-------| | Normalité| shapiro.test | variable | [ici](#shapiro) | | Homoscédasticité | bartlett.test | variable~facteur| [ici](#bartlett) | | Homoscédasticité | levene.test | variable, facteur, location | [ici](#levene) | :Exemple {#shapiro, toggle=popup} La fonction ` shapiro.test()` est disponible dans le package `car`. ```r library(car) ``` ``` ## Le chargement a nécessité le package : carData ``` ```r shapiro.test(resid(modele)) ``` ``` ## ## Shapiro-Wilk normality test ## ## data: resid(modele) ## W = 0.96982, p-value = 0.8553 ``` La p-value (environ égale à 0.86) est supérieure à 5 % donc on ne rejette pas l'hypothèse de normalité de la distribution des résidus. :Exemple {#bartlett, toggle=popup} ```r bartlett.test(resid(modele)~donnees$Cepage) ``` ``` ## ## Bartlett test of homogeneity of variances ## ## data: resid(modele) by donnees$Cepage ## Bartlett's K-squared = 1.9725, df = 2, p-value = 0.373 ``` La p-value (environ égale à 0.37) est supérieure à 5 % donc on ne rejette pas l'hypothèse d'homoscédasticité des distributions des résidus. :Exemple {#levene, toggle=popup} La fonction ` levene.test()` est disponible dans le package `lawstat`. L'argument "location" correspond à la moyenne ou à la médiane (location=c("median", "mean")). Test de Levene sur les moyennes : ```r library("lawstat") ``` ``` ## Warning: le package 'lawstat' a été compilé avec la version R 4.1.2 ``` ```r levene.test(resid(modele), donnees$Cepage, location="mean") ``` ``` ## ## Classical Levene's test based on the absolute deviations from the mean ## ( none not applied because the location is not set to median ) ## ## data: resid(modele) ## Test Statistic = 1.6952, p-value = 0.2247 ``` La p-value (environ égale à 0.22) est supérieure à 5 % donc on ne rejette pas l'hypothèse de normalité de la distribution des résidus. Le test de Levene (test de Brown-Forsythe sur les médianes) peut s'obtenir en utilisant : ```r levene.test(resid(modele), donnees$Cepage, location="median") ``` ``` ## ## Modified robust Brown-Forsythe Levene-type test based on the absolute ## deviations from the median ## ## data: resid(modele) ## Test Statistic = 1.6618, p-value = 0.2306 ``` :Suite ANOVA {#anova, toggle=collapse} [ANOVA à un facteur : représentations graphiques](caps_12_1_anova1_gestion_graphiques.html) [ANOVA à un facteur : Réalisation et Vérification des hypothèses](caps_12_2_anova1_hypotheses.html) [ANOVA à un facteur : Récupération des résultats du tableau d'ANOVA](caps_12_3_anova1_resultats.html) [ANOVA à un facteur : Tests de comparaison post-hoc](caps_12_4_anova1_posthoc.html) [ANOVA à plusieurs facteurs](caps_12_5_anova_mult_posthoc.html) [Exercice bilan](caps_12_6_anova_exbilan.html)