Begin'R
Les statistiques avec R
Navigation
[Retour au sommaire]
# Choix du nombre d'axes pour l'interprétation d'une ACP :Objectifs {#ACP4} * Extraire les valeurs propres d'une ACP * Choisir le nombre d'axes factoriels pour interpréter une ACP :Remarque : Besoin de quelques rappels pour l'importation et la préparation du jeu de données? {#rq_ACP_presentation_jeu_donnees_avec_ACP_normee, toggle=collapse, title-display=show} Le jeu de données utilisé dans les exemples est celui sur les données `Tomates`. Les liens ci-dessous permettent de télécharger les fichiers de données, de voir une description associée et d'obtenir les lignes de code pour importer le jeu de données sur R. | Jeu de données | Excel | CSV | Présentation | Commande R | Explication | |----------------|--------|-------------|----------------|------------|-------------| | Données Tomates | [](donnees/DonneesTomates.xlsx) | [](donnees/DonneesTomates.csv) | [Tomates](#tomatesexp) | [Importer le jeu de données](#ligne_code_importation_tomates) | [Préparation du jeu de données Tomates](#explication_preparation_importation_tomates) | :Exemple{#tomatesexp, toggle=popup, title-display=hidden} Un jeu de données sur la tomate, issu d'une étude expérimentale de l'UMR 1332 Biologie du fruit et Pathologie (Centre INRA Bordeaux-Nouvelle Aquitaine) est considéré. L'objectif est de repérer les facteurs qui influencent le calibre des fruits de tomate. Les données se présentent sous la forme d'un tableau Individus (en lignes) x Variables (en colonnes). Chaque individu statistique correspond à un individu-fruit dont les caractéristiques sont présentées en ligne. Les individus sont décrits par 7 variables, dont 2 qualitatives (nominales ou ordinales) et 5 quantitatives (numériques) présentées en colonnes. * La variable `Genotype` (qualitative nominale): Génotype de plante de tomate sur laquelle le fruit a été récolté. Il s'agit soit de plantes de type sauvage (C), soit de lignées transgéniques (L) ; * La variable `Stade` (qualitative ordinale): Stades de développement du fruit. Les stades 1 à 3 sont des stade de croissance (fruits verts) et les stades 4 et 5 des stades de maturité (fruits rouges); * La variable `Aire_Pericarpe` (quantitative): Aire du péricarpe, la partie charnue du fruit de tomate sans le gel (en mm²) ; * La variable `PerimetreExt_Fruit` (quantitative): Périmètre externe des fruits de tomate (en mm) ; * La variable `DiametreExt_Fruit` (quantitative): Diamètre des fruits de tomate (en mm) ; * La variable `Epaisseur_Pericarpe` (quantitative): Epaisseur du péricarpe, la partie charnue du fruit de tomate sans le gel, (en mm) ; * La variable `Nombre_Loge` (quantitative): Nombre de loges dans le fruit de tomate en coupe transversale. :Exemple {#ligne_code_importation_vins, toggle=popup} ```r Donnees <- read.csv2("DonneesVins.csv", header = TRUE, stringsAsFactors = TRUE) X <- Donnees[, 4:11] library("FactoMineR") res.pca <- PCA(X, scale.unit = TRUE, graph = FALSE) ``` :Exemple {#ligne_code_importation_tomates, toggle=popup} ```r Donnees <- read.csv2("DonneesTomates.csv", header = TRUE, stringsAsFactors = TRUE) X <- Donnees[, 4:8] library("FactoMineR") res.pca <- PCA(X, scale.unit = TRUE, graph = FALSE) ``` :Exemple {#explication_preparation_importation_tomates, toggle=popup} Dans un premier temps, [importer le jeu de données tomates sur R Studio](caps_2_3_importation_CSV.html). ```r Donnees <- read.csv2("DonneesTomates.csv", header = TRUE, stringsAsFactors = TRUE) ``` Les 6 premiers individus sont affichés ci-dessous : ``` ## Nom Genotype Stade Aire_Pericarpe PerimetreExt_Fruit DiametreExt_Fruit ## 1 C1st1_1 C1 st1 105.43 62.08 19.68 ## 2 C1st1_2 C1 st1 38.60 41.31 13.11 ## 3 C1st1_3 C1 st1 34.47 41.01 13.00 ## 4 C1st2_1 C1 st2 578.09 134.43 42.66 ## 5 C1st2_2 C1 st2 509.71 126.82 40.11 ## 6 C1st2_3 C1 st2 622.92 137.36 43.41 ## Epaisseur_Pericarpe Nombre_Loge ## 1 1.74 2 ## 2 1.00 2 ## 3 0.82 3 ## 4 4.55 3 ## 5 4.33 2 ## 6 4.95 2 ``` Pour appliquer une méthode d'analyse de données multivariées (analyse en composantes principales, classification ascendante hiérarchique, classification par la méthode des centres mobiles), il faut extraire du jeu de données uniquement les variables quantitatives. Pour ce jeu de données, comme elles se trouvent sur les colonnes 4 à 8, il faut utiliser l'instruction suivante pour [extraire les colonnes du jeu de données](caps_2_9_extraire_sous_ensemble.html): ```r X <- Donnees[, 4:8] ``` La variable `X` contient ainsi uniquement les variables quantitatives. Les 6 premiers individus sont affichés ci-dessous ``` ## Aire_Pericarpe PerimetreExt_Fruit DiametreExt_Fruit Epaisseur_Pericarpe ## 1 105.43 62.08 19.68 1.74 ## 2 38.60 41.31 13.11 1.00 ## 3 34.47 41.01 13.00 0.82 ## 4 578.09 134.43 42.66 4.55 ## 5 509.71 126.82 40.11 4.33 ## 6 622.92 137.36 43.41 4.95 ## Nombre_Loge ## 1 2 ## 2 2 ## 3 3 ## 4 3 ## 5 2 ## 6 2 ``` Une ACP normée est ensuite mise en place comme vu dans [cette capsule](caps_13_3bis_ACP_mise_en_place_ACP.html). ```r library("FactoMineR") res.pca <- PCA(X, scale.unit = TRUE, graph = FALSE) ``` Le tableau ci-dessous présente les fonctions R pour extraire les valeurs propres d'une ACP et afficher le graphique des éboulis | Rôle | Commande R | Arguments | Exemple | |-------------------------------------------------------|--------------------|-------------------------|------------------------| | Calculer les valeurs propres | `get_eigenvalue()` | | [ici](#exemple_valeurs_propres) | | Afficher le graphique des éboulis | `fviz_eig()` | `addlabels`, `ylim` | [ici](#exemple_graphique_eboulis) | :Exemple {#exemple_valeurs_propres, toggle=popup} La fonction `get_eigenvalue()` permet d'extraire les valeurs propres d'une ACP. Comme cette fonction fait partie du package `factoextra`, il faut au préalable [installer et charger ce package](caps_1_6_packages.html). Dans la fonction `get_eigenvalue()`, le premier argument correspond au résultat de la fonction `PCA()`. ```r library("factoextra") eig.val <- get_eigenvalue(res.pca) eig.val ``` ``` ## eigenvalue variance.percent cumulative.variance.percent ## Dim.1 4.035552e+00 8.071105e+01 80.71105 ## Dim.2 9.008564e-01 1.801713e+01 98.72818 ## Dim.3 5.333376e-02 1.066675e+00 99.79485 ## Dim.4 1.024232e-02 2.048464e-01 99.99970 ## Dim.5 1.513639e-05 3.027278e-04 100.00000 ``` Les composantes principales sont représentées sur les lignes et les trois colonnes correspondent respectivement aux valeurs propres, aux pourcentagse de variance expliquée et aux pourcentages cumulés de variance expliquée. Dans ce jeu de données `Tomates`, les deux premières composantes principales expliquent respectivement 80% et 18% de la variance du jeu de données. Ces deux composantes principales seront retenues pour l'analyse de ce jeu de données. :Exemple {#exemple_graphique_eboulis, toggle=popup} La fonction `fviz_eig()` permet d'afficher le graphique des éboulis afin de visualiser la décroissance des valeurs propres. Comme cette fonction fait partie du package `factoextra`, il faut au préalable [installer et charger ce package](caps_1_6_packages.html). Dans la fonction `fviz_eig()`, le premier argument correspond au résultat de la fonction `PCA()`. L'argument `addlabels=TRUE` permet d'ajouter les valeurs du pourcentage de variance expliquée par chaque composante principale. L'argument `ylim = c(0, 100)` permet de spécifier que l'axe des ordonnées va de 0 à 100. ```r library("factoextra") fviz_eig(res.pca, addlabels = TRUE, ylim = c(0, 100), main = "Graphique des éboulis", xlab = "Composante principale", ylab = "Pourcentage de variance expliquée") ``` 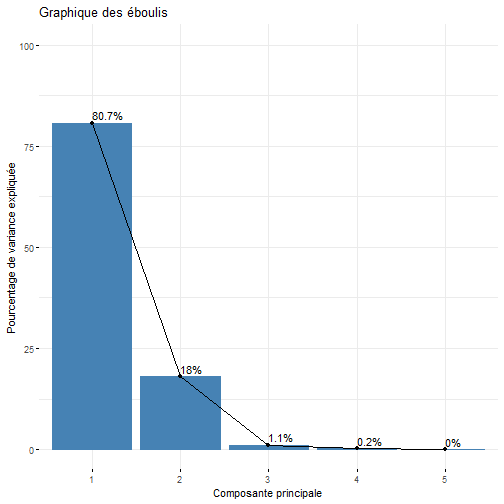 :suite ACP {#ACP, toggle=collapse} [Choix de la métrique](caps_13_2_acp_metrique.html) [Calcul et visualisation de la matrice de corrélation](caps_13_3_acp_matrice_correlation.html) [Mise en place de l'analyse en composantes principales](caps_13_3bis_acp_mise_en_place_acp.html) [Choix du nombre d'axes pour l'interprétation](caps_13_4_acp_valeurs_propres.html) [Analyse du cercle des corrélations](caps_13_5_acp_cercle_correlation.html) [Analyse du graphique des individus](caps_13_6_acp_graphique_individus.html) [Exercice bilan](caps_13_7_acp_exercice_bilan.html)