Begin'R
Les statistiques avec R
Navigation
[Retour au sommaire]
# Etude du cercle des corrélations d'une ACP :Objectifs {#ACP5} * Afficher le cercle de corrélation * Décrire les composantes principales :Remarque : Besoin de quelques rappels pour l'importation et la préparation du jeu de données? {#rq_ACP_presentation_jeu_donnees_avec_ACP_normee, toggle=collapse, title-display=show} Le jeu de données utilisé dans les exemples est celui sur les données `Tomates`. Les liens ci-dessous permettent de télécharger les fichiers de données, de voir une description associée et d'obtenir les lignes de code pour importer le jeu de données sur R. | Jeu de données | Excel | CSV | Présentation | Commande R | Explication | |----------------|--------|-------------|----------------|------------|-------------| | Données Tomates | [](donnees/DonneesTomates.xlsx) | [](donnees/DonneesTomates.csv) | [Tomates](#tomatesexp) | [Importer le jeu de données](#ligne_code_importation_tomates) | [Préparation du jeu de données Tomates](#explication_preparation_importation_tomates) | :Exemple{#tomatesexp, toggle=popup, title-display=hidden} Un jeu de données sur la tomate, issu d'une étude expérimentale de l'UMR 1332 Biologie du fruit et Pathologie (Centre INRA Bordeaux-Nouvelle Aquitaine) est considéré. L'objectif est de repérer les facteurs qui influencent le calibre des fruits de tomate. Les données se présentent sous la forme d'un tableau Individus (en lignes) x Variables (en colonnes). Chaque individu statistique correspond à un individu-fruit dont les caractéristiques sont présentées en ligne. Les individus sont décrits par 7 variables, dont 2 qualitatives (nominales ou ordinales) et 5 quantitatives (numériques) présentées en colonnes. * La variable `Genotype` (qualitative nominale): Génotype de plante de tomate sur laquelle le fruit a été récolté. Il s'agit soit de plantes de type sauvage (C), soit de lignées transgéniques (L) ; * La variable `Stade` (qualitative ordinale): Stades de développement du fruit. Les stades 1 à 3 sont des stade de croissance (fruits verts) et les stades 4 et 5 des stades de maturité (fruits rouges); * La variable `Aire_Pericarpe` (quantitative): Aire du péricarpe, la partie charnue du fruit de tomate sans le gel (en mm²) ; * La variable `PerimetreExt_Fruit` (quantitative): Périmètre externe des fruits de tomate (en mm) ; * La variable `DiametreExt_Fruit` (quantitative): Diamètre des fruits de tomate (en mm) ; * La variable `Epaisseur_Pericarpe` (quantitative): Epaisseur du péricarpe, la partie charnue du fruit de tomate sans le gel, (en mm) ; * La variable `Nombre_Loge` (quantitative): Nombre de loges dans le fruit de tomate en coupe transversale. :Exemple {#ligne_code_importation_vins, toggle=popup} ```r Donnees <- read.csv2("DonneesVins.csv", header = TRUE, stringsAsFactors = TRUE) X <- Donnees[, 4:11] library("FactoMineR") res.pca <- PCA(X, scale.unit = TRUE, graph = FALSE) ``` :Exemple {#ligne_code_importation_tomates, toggle=popup} ```r Donnees <- read.csv2("DonneesTomates.csv", header = TRUE, stringsAsFactors = TRUE) X <- Donnees[, 4:8] library("FactoMineR") res.pca <- PCA(X, scale.unit = TRUE, graph = FALSE) ``` :Exemple {#explication_preparation_importation_tomates, toggle=popup} Dans un premier temps, [importer le jeu de données tomates sur R Studio](caps_2_3_importation_CSV.html). ```r Donnees <- read.csv2("DonneesTomates.csv", header = TRUE, stringsAsFactors = TRUE) ``` Les 6 premiers individus sont affichés ci-dessous : ``` ## Nom Genotype Stade Aire_Pericarpe PerimetreExt_Fruit DiametreExt_Fruit ## 1 C1st1_1 C1 st1 105.43 62.08 19.68 ## 2 C1st1_2 C1 st1 38.60 41.31 13.11 ## 3 C1st1_3 C1 st1 34.47 41.01 13.00 ## 4 C1st2_1 C1 st2 578.09 134.43 42.66 ## 5 C1st2_2 C1 st2 509.71 126.82 40.11 ## 6 C1st2_3 C1 st2 622.92 137.36 43.41 ## Epaisseur_Pericarpe Nombre_Loge ## 1 1.74 2 ## 2 1.00 2 ## 3 0.82 3 ## 4 4.55 3 ## 5 4.33 2 ## 6 4.95 2 ``` Pour appliquer une méthode d'analyse de données multivariées (analyse en composantes principales, classification ascendante hiérarchique, classification par la méthode des centres mobiles), il faut extraire du jeu de données uniquement les variables quantitatives. Pour ce jeu de données, comme elles se trouvent sur les colonnes 4 à 8, il faut utiliser l'instruction suivante pour [extraire les colonnes du jeu de données](caps_2_9_extraire_sous_ensemble.html): ```r X <- Donnees[, 4:8] ``` La variable `X` contient ainsi uniquement les variables quantitatives. Les 6 premiers individus sont affichés ci-dessous ``` ## Aire_Pericarpe PerimetreExt_Fruit DiametreExt_Fruit Epaisseur_Pericarpe ## 1 105.43 62.08 19.68 1.74 ## 2 38.60 41.31 13.11 1.00 ## 3 34.47 41.01 13.00 0.82 ## 4 578.09 134.43 42.66 4.55 ## 5 509.71 126.82 40.11 4.33 ## 6 622.92 137.36 43.41 4.95 ## Nombre_Loge ## 1 2 ## 2 2 ## 3 3 ## 4 3 ## 5 2 ## 6 2 ``` Une ACP normée est ensuite mise en place comme vu dans [cette capsule](caps_13_3bis_ACP_mise_en_place_ACP.html). ```r library("FactoMineR") res.pca <- PCA(X, scale.unit = TRUE, graph = FALSE) ``` Le tableau ci-dessous présente les fonctions R pour afficher le cercle des corrélations et visualiser la contribution des variables aux composantes principales. | Rôle | Commande R | Arguments | Exemple | |-------------------------------------------------------|--------------------|-------------------------|------------------------| | Afficher le cercle de corrélation | `fviz_pca_var()` | `axes`, `col.var`, `gradient.cols`, `repel` | [ici](#exemple_cercle_correlation) | | Calculer la contribution des variables aux composantes principales | `get_pca_var()` | | [ici](#exemple_contribution_variables) | | Décrire les composantes principales | `dimdesc()` | `proba` | [ici](#exemple_dimdesc) | :Exemple {#exemple_cercle_correlation, toggle=popup} La fonction `fviz_pca_var()` permet d'afficher le cercle de corrélation. Comme cette fonction fait partie du package `factoextra`, il faut au préalable [installer et charger ce package](caps_1_6_packages.html). Dans la fonction `fviz_pca_var()`, le premier argument correspond au résultat de la fonction `PCA()`. L'argument `axes` est un vecteur de 2 valeurs numériques contenant le numéro des composantes principales à observer. Ici, les deux premières composantes principales sont représentées. L'argument `col.var = "cos2"` permet d'afficher les variables selon leur qualité de représentation avec la palette de couleur fournie par `gradient.cols = c("blue", "orange", "red")`. Dans la figure ci-dessous, les variables les mieux représentées (les plus proches du cercle unité) sont en rouge. Tandis que les plus "éloignées" sont en bleu. L'argument `repel = TRUE` permet d'éviter le chevauchement du texte sur le graphique. ```r library("factoextra") fviz_pca_var(res.pca, axes = c(1,2), col.var = "cos2", gradient.cols = c("blue", "orange", "red"), repel = TRUE) ``` 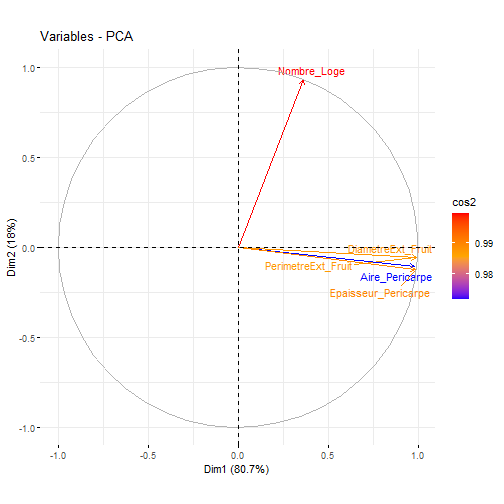 Toutes les variables sont très bien représentées sur les deux premières composantes principales. Comme observée dans la [matrice de corrélation](caps_13_3_acp_matrice_correlation.html) une très forte corrélation est mise en évidence entre les variables `Aire_Pericarpe`, `PerimetreExt_Fruit`, `DiametreExt_Fruit` et `Epaisseur_Pericarpe`. :Exemple {#exemple_contribution_variables, toggle=popup} La fonction `get_pca_var()` permet de récupérer la contribution des variables aux composantes principales (`var$contrib`). La fonction `corrplot()` permet ensuite de visualiser graphiquement cette information. Pour cette dernière fonction, il faut spécifier `is.corr=FALSE` car `var$contrib` n'est pas une matrice de corrélation. ```r library("factoextra") library("corrplot") var <- get_pca_var(res.pca) corrplot(var$contrib, is.corr=FALSE) ``` 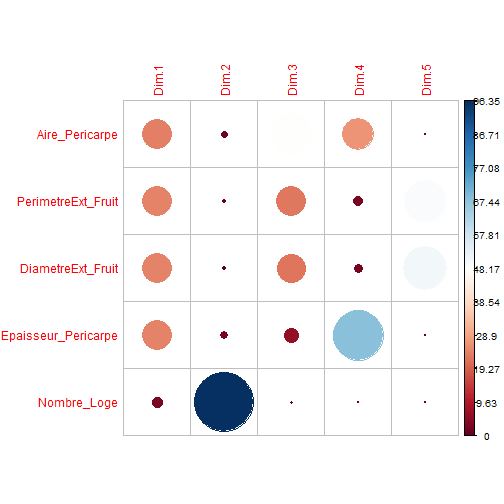 Ce graphique montre bien que les variables `Aire_Pericarpe`, `PerimetreExt_Fruit`, `DiametreExt_Fruit` et `Epaisseur_Pericarpe` contribuent à part égales à la première composante principale, tandis que la variable `Nombre_Loge` contribue à la deuxième composante principale. Il est inutile d'essayer d'interpréter les composantes principales suivantes car elles [expliquent très peu de variance](caps_13_4_acp_valeurs_propres.html). :Exemple {#exemple_dimdesc, toggle=popup} La fonction `dimdesc()` permet de décrire les composantes principales. Comme cette fonction fait partie du package `FactoMineR`, il faut au préalable [installer et charger ce package](caps_1_6_packages.html). Dans la fonction `dimdesc()`, le premier argument correspond au résultat de la fonction `PCA()`. L'argument `proba` correspond au risque $\alpha$ de premier espèce pour le test de corrélation entre une variable et une composante principale. $\$$Dim.1$\$$quanti contient en ligne la liste des variables quantitatives qui contribuent à la première composante principale. En colonne sont affichées la valeur du coefficient corrélation entre la variable et la première composante principale, ainsi que la p-value du test de corrélation. Toutes les variables conduisant au rejet de l'hypothèse $\mathcal{H}0$ sont affichées, c'est-à-dire celles dont la p-value est inférieure au risque $\alpha$. De la même façon, $\$$Dim.2$\$$quanti contient la liste des variables quantitatives contribuant à la deuxième composante principale. ```r library("FactoMineR") dimdesc(res.pca, proba = 0.05) ``` ``` ## $Dim.1 ## $quanti ## correlation p.value ## DiametreExt_Fruit 0.9922904 2.671051e-54 ## PerimetreExt_Fruit 0.9920458 6.586012e-54 ## Epaisseur_Pericarpe 0.9870931 7.691310e-48 ## Aire_Pericarpe 0.9800551 2.116414e-42 ## Nombre_Loge 0.3631756 4.343827e-03 ## ## attr(,"class") ## [1] "condes" "list" ## ## $Dim.2 ## $quanti ## correlation p.value ## Nombre_Loge 0.9316337 3.550197e-27 ## ## attr(,"class") ## [1] "condes" "list" ## ## $Dim.3 ## named list() ## attr(,"class") ## [1] "condes" "list" ## ## $call ## $call$num.var ## [1] 1 ## ## $call$proba ## [1] 0.05 ## ## $call$weights ## [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ## [39] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ## ## $call$X ## Dim.1 Aire_Pericarpe PerimetreExt_Fruit DiametreExt_Fruit ## 1 -2.9275367 105.43 62.08 19.68 ## 2 -3.4492985 38.60 41.31 13.11 ## 3 -3.1200537 34.47 41.01 13.00 ## 4 -0.5001288 578.09 134.43 42.66 ## 5 -1.0914665 509.71 126.82 40.11 ## 6 -0.7197763 622.92 137.36 43.41 ## 7 1.2202819 1201.34 178.73 56.57 ## 8 1.3776409 1240.41 191.71 60.80 ## 9 1.1018973 1136.19 179.73 56.90 ## 10 1.5889499 1498.33 197.00 62.58 ## 11 1.3463420 1386.92 193.32 61.39 ## 12 1.2553420 1346.46 189.74 60.29 ## 13 1.2204636 1347.50 186.81 59.16 ## 14 1.4434088 1313.35 175.26 55.83 ## 15 2.3146645 1889.25 205.49 65.19 ## 16 -3.5577842 34.75 33.63 10.65 ## 17 -3.4896993 37.75 38.97 12.31 ## 18 -3.5220329 37.08 36.47 11.60 ## 19 -0.8176423 596.20 133.91 42.50 ## 20 -1.0602213 552.47 120.11 38.12 ## 21 -0.8505620 597.73 131.39 41.77 ## 22 0.5729272 1091.24 174.04 55.21 ## 23 1.0412798 1103.59 179.55 56.79 ## 24 0.8060422 1021.08 174.27 55.13 ## 25 1.8714718 1594.69 209.94 66.49 ## 26 1.5439324 1304.78 193.45 61.42 ## 27 1.4112743 1253.22 186.25 59.20 ## 28 1.1756691 1328.90 185.22 58.79 ## 29 1.7905038 1588.25 200.88 63.54 ## 30 1.6928049 1567.64 197.21 62.51 ## 31 -3.6091067 30.72 31.93 10.13 ## 32 -3.3291050 53.21 45.12 14.29 ## 33 -3.5863681 28.31 34.84 11.04 ## 34 -1.0207981 517.15 132.40 41.92 ## 35 -0.6471562 541.15 127.32 40.39 ## 36 -1.0468677 527.51 126.60 40.20 ## 37 0.2580087 973.54 165.34 52.20 ## 38 1.2288908 1180.75 188.56 59.48 ## 39 0.2793737 971.99 169.15 53.75 ## 40 1.2732361 1209.60 179.63 57.07 ## 41 1.2842583 1369.48 190.28 60.10 ## 42 1.2304321 1168.84 179.33 57.08 ## 43 2.2868276 1652.00 201.04 63.77 ## 44 1.7880589 1616.43 195.88 62.18 ## 45 2.4060407 1716.02 202.90 64.48 ## 46 -3.5359315 33.22 36.50 11.51 ## 47 -3.0323931 43.26 44.31 14.07 ## 48 -3.6828629 21.80 31.06 9.84 ## 49 -1.2942086 475.76 113.51 36.07 ## 50 -1.4430508 423.00 112.11 35.58 ## 51 -0.8410254 481.88 124.09 39.41 ## 52 1.1547194 1156.00 183.34 58.11 ## 53 0.4016174 1028.90 167.41 53.13 ## 54 0.7378759 985.97 172.66 54.59 ## 55 1.9684638 1453.90 204.30 64.85 ## 56 1.2959061 1385.37 187.07 59.45 ## 57 1.3898764 1254.70 187.66 59.35 ## 58 2.7152848 1840.39 211.76 67.34 ## 59 3.2482992 2035.89 238.07 75.77 ## 60 2.4530102 1871.05 219.11 69.58 ## Epaisseur_Pericarpe Nombre_Loge ## 1 1.74 2 ## 2 1.00 2 ## 3 0.82 3 ## 4 4.55 3 ## 5 4.33 2 ## 6 4.95 2 ## 7 7.36 3 ## 8 6.84 3 ## 9 6.89 3 ## 10 8.45 2 ## 11 7.93 2 ## 12 7.93 2 ## 13 8.03 2 ## 14 8.39 3 ## 15 9.99 2 ## 16 1.12 2 ## 17 1.00 2 ## 18 1.04 2 ## 19 4.81 2 ## 20 4.92 2 ## 21 4.84 2 ## 22 6.70 2 ## 23 6.72 3 ## 24 6.25 3 ## 25 8.43 2 ## 26 7.32 3 ## 27 7.47 3 ## 28 7.99 2 ## 29 8.86 2 ## 30 8.72 2 ## 31 1.00 2 ## 32 1.27 2 ## 33 0.87 2 ## 34 4.17 2 ## 35 4.55 3 ## 36 4.50 2 ## 37 6.30 2 ## 38 6.61 3 ## 39 6.02 2 ## 40 7.51 3 ## 41 7.99 2 ## 42 7.47 3 ## 43 9.25 3 ## 44 9.15 2 ## 45 9.44 3 ## 46 0.99 2 ## 47 0.97 3 ## 48 0.70 2 ## 49 4.55 2 ## 50 4.08 2 ## 51 4.01 3 ## 52 6.75 3 ## 53 6.63 2 ## 54 6.18 3 ## 55 8.04 3 ## 56 8.23 2 ## 57 7.25 3 ## 58 9.79 3 ## 59 9.44 3 ## 60 9.58 2 ``` :suite ACP {#ACP, toggle=collapse} [Choix de la métrique](caps_13_2_acp_metrique.html) [Calcul et visualisation de la matrice de corrélation](caps_13_3_acp_matrice_correlation.html) [Mise en place de l'analyse en composantes principales](caps_13_3bis_acp_mise_en_place_acp.html) [Choix du nombre d'axes pour l'interprétation](caps_13_4_acp_valeurs_propres.html) [Analyse du cercle des corrélations](caps_13_5_acp_cercle_correlation.html) [Analyse du graphique des individus](caps_13_6_acp_graphique_individus.html) [Exercice bilan](caps_13_7_acp_exercice_bilan.html)