Begin'R
Les statistiques avec R
Navigation
[Retour au sommaire]
# Exercice bilan :Objectifs {#ACP7} * Evaluer ses compétences sur l'analyse en composantes principales. :Exercice : Analyse du jeu de données sur les vins {#exercice_ACP_vins} Le jeu de données utilisé dans cet exercice est celui sur les `Vins`. Les liens ci-dessous permettent de télécharger les fichiers de données, de visionner une vidéo expliquant la description associée et d'obtenir les lignes de code pour importer le jeu de données sur R. | Jeu de données | Excel | CSV | Présentation | Commande R | Explication | |----------------|--------|-------------|----------------|------------|-------------| | Donneées Vins | [](donnees/DonneesVins.xlsx) | [](donnees/DonneesVins.csv) | [](video/DonneesVins.html) | [Importer le jeu de données](#ligne_code_importation_vins) | [Préparation du jeu de données Vins](#explication_preparation_importation_vins) | :Exemple {#ligne_code_importation_vins, toggle=popup} ```r Donnees <- read.csv2("DonneesVins.csv", header = TRUE, stringsAsFactors = TRUE) X <- Donnees[, 4:11] ``` :Exemple {#explication_preparation_importation_vins, toggle=popup} Dans un premier temps, [importer le jeu de données vins sur R Studio](caps_2_3_importation_csv.html). ```r Donnees <- read.csv2("DonneesVins.csv", header = TRUE, stringsAsFactors = TRUE) ``` Les 6 premiers individus sont affichés ci-dessous : ``` ## Origine Couleur Libelle Alcool pH AcTot Tartrique Malique Citrique ## 1 Bordeaux Blanc 1 12.0 2.84 89 21.1 21.0 4.3 ## 2 Bordeaux Blanc 2 11.5 3.10 97 26.4 34.2 3.9 ## 3 Bordeaux Blanc 3 14.6 2.96 99 20.7 21.8 8.1 ## 4 Bordeaux Blanc 4 10.5 3.10 72 29.7 4.2 3.6 ## 5 Bordeaux Blanc 5 14.0 3.29 76 22.3 9.3 4.7 ## 6 Bordeaux Blanc 6 13.2 2.94 83 24.6 9.4 4.1 ## Acetique Lactique ## 1 16.9 9.3 ## 2 9.9 16.0 ## 3 19.7 11.2 ## 4 11.9 14.4 ## 5 20.1 21.6 ## 6 19.7 16.8 ``` Pour appliquer une méthode d'analyse de données multivariées (analyse en composantes principales, classification ascendante hiérarchique, classification par la méthode des centres mobiles), il faut extraire du jeu de données uniquement les variables quantitatives. Pour ce jeu de données, comme elles se trouvent sur les colonnes 4 à 11, il faut utiliser l'instruction suivante pour [extraire les colonnes du jeu de données](caps_2_9_extraire_sous_ensemble.html): ```r X <- Donnees[, 4:11] ``` La variable X contient ainsi uniquement les variables quantitatives. Les 6 premiers individus sont affichés ci-dessous ``` ## Alcool pH AcTot Tartrique Malique Citrique Acetique Lactique ## 1 12.0 2.84 89 21.1 21.0 4.3 16.9 9.3 ## 2 11.5 3.10 97 26.4 34.2 3.9 9.9 16.0 ## 3 14.6 2.96 99 20.7 21.8 8.1 19.7 11.2 ## 4 10.5 3.10 72 29.7 4.2 3.6 11.9 14.4 ## 5 14.0 3.29 76 22.3 9.3 4.7 20.1 21.6 ## 6 13.2 2.94 83 24.6 9.4 4.1 19.7 16.8 ``` 1. Quelle métrique utiliser pour analyser ce jeu de données ? :Corrigé {#answer_ACP_vins1, toggle=collapse, title-display=show} Pour choisir quelle métrique utiliser, il faut regarder la variabilité des variables. Pour cela, la fonction `numSummary()` permet d'estimer les écart-types. ```r library(RcmdrMisc) numSummary(data = X, statistics = c("mean", "sd")) ``` ``` ## mean sd n ## Alcool 12.350000 1.3751883 36 ## pH 3.227500 0.2461286 36 ## AcTot 86.055556 13.4460710 36 ## Tartrique 30.825000 8.4322298 36 ## Malique 12.011111 12.4689277 36 ## Citrique 3.288889 2.0514494 36 ## Acetique 15.669444 3.8055463 36 ## Lactique 19.902778 8.8735397 36 ``` Les écarts-types étant très différents. Il est nécessaire de normaliser les variables. La métrique des inverses des variances est donc utilisée pour analyser ce jeu de données. De plus, comme les 8 variables quantitatives décrivent des grandeurs physico-chimiques différentes, exprimées dans des unités différentes, il est indispensable de travailler sur les variables centrées réduites. 2. Afficher le corrélogramme. :Corrigé {#answer_ACP_vins2, toggle=collapse, title-display=show} 2. Le corrélogramme s'obtient en calculant d'abord la matrice de corrélation puis ensuite en utilisant la fonction `corrplot()`. ```r library(corrplot) M <- cor(X, method = "pearson") corrplot(M, type="upper", order="hclust", tl.col="black", tl.srt=45) ``` 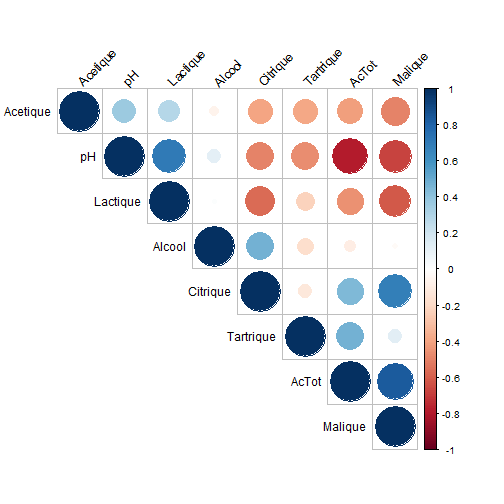 3. Mettre en place l'analyse en composantes principales. :Corrigé {#answer_ACP_vins3, toggle=collapse, title-display=show} 3. Comme la métrique des inverses des variances a été choisie pour analyser ce jeu de données, une ACP normée doit être mise en place. Pour cela, il faut utiliser la fonction `PCA()` en spécifiant l'argument `scale.unit = TRUE`. ```r library("FactoMineR") res.pca <- PCA(X, scale.unit = TRUE, graph = FALSE) ``` 4. Combien de composantes principales faut-il conserver pour expliquer au moins 80% de la variance du jeu de données ? :Corrigé {#answer_ACP_vins4, toggle=collapse, title-display=show} 4. Grâce au résumé ci-dessous, les 3 premières composantes principales sont nécessaires pour expliquer 80.7% de la variance du jeu de données. ```r library("factoextra") eig.val <- get_eigenvalue(res.pca) eig.val ``` ``` ## eigenvalue variance.percent cumulative.variance.percent ## Dim.1 3.93927870 49.2409837 49.24098 ## Dim.2 1.58261946 19.7827433 69.02373 ## Dim.3 0.93652089 11.7065112 80.73024 ## Dim.4 0.66679995 8.3349993 89.06524 ## Dim.5 0.53214113 6.6517641 95.71700 ## Dim.6 0.18582517 2.3228146 98.03982 ## Dim.7 0.13028334 1.6285417 99.66836 ## Dim.8 0.02653137 0.3316421 100.00000 ``` ```r fviz_eig(res.pca, addlabels = TRUE, ylim = c(0, 60), main = "Graphique des éboulis", xlab = "Composante principale", ylab = "Pourcentage de variance expliquée") ``` 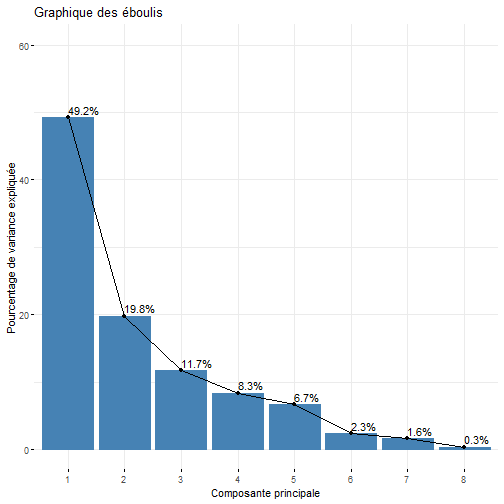 5. Afficher le cercle des corrélations sur les composantes principales $C_1$ et $C_2$, puis sur $C_1$ et $C_3$. :Corrigé {#answer_ACP_vins5, toggle=collapse, title-display=show} 5. Pour choisir les axes factoriels à représenter sur le cercle de corrélation, il suffit de modifier l'argument `axes` de la fonction `fviz_pca_var()`. Il faut choisir `axes = c(1,2)` pour afficher le cercle de corrélations sur le premier plan factoriel $C_1$-$C_2$ (noté `Dim1` et `Dim2` sur le graphique ci-dessous). ```r fviz_pca_var(res.pca, axes = c(1,2), col.var = "cos2", gradient.cols = c("blue", "orange", "red"), repel = TRUE) ``` 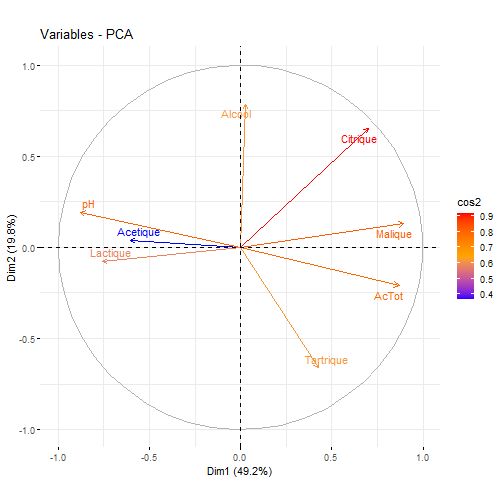 Et `axes = c(1,3)` pour visualiser le cercle des corrélations sur les composantes principales $C_1$ et $C_3$ (notée `Dim1` et `Dim3` sur la figure). ```r fviz_pca_var(res.pca, axes = c(1,3), col.var = "cos2", gradient.cols = c("blue", "orange", "red"), repel = TRUE) ``` 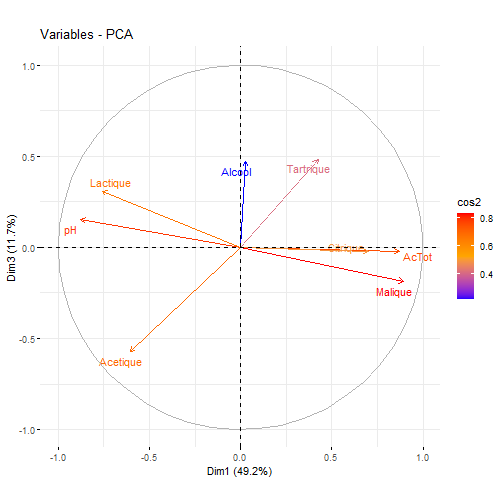 6. Quelles variables contribuent significativement à la première composante principale. Donner un sens physique à cette composante principale. :Corrigé {#answer_ACP_vins6, toggle=collapse, title-display=show} 6. Les variables qui contribuent significativement à la première composante principale sont obtenues à l'aide de la fonction `dimdesc()` : ```r description = dimdesc(res.pca, proba = 0.05) description$Dim.1$quanti ``` ``` ## correlation p.value ## Malique 0.8939000 2.142707e-13 ## AcTot 0.8686655 6.588497e-12 ## Citrique 0.7019301 1.838453e-06 ## Tartrique 0.4256968 9.639662e-03 ## Acetique -0.6051259 9.240493e-05 ## Lactique -0.7583124 8.444896e-08 ## pH -0.8773273 2.214122e-12 ``` Comme l'acidité totale (`AcTot`) contribue positivement (et le `pH` négativement) à la première composante principale. Cet axe factoriel traduit l'acidité de vins. Cet axe traduit également le degré d'avancement dans la fermentation malo-lactique, fermentation durant laquelle l'acide malique est transformé en acide lactique. 7. Représenter l'information sur la `Couleur` puis sur l'`Origine` dans le graphique des individus sur les composantes principales $C_1$ et $C_2$. :Corrigé {#answer_ACP_vins7, toggle=collapse, title-display=show} 7. Le graphique ci-dessous met clairement en évidence un effet `Couleur` sur la première composante principale. Les vins blancs sont majoritairement représentés à droite du graphique des individus, tandis que les vins rouges sont sur la partie gauche. ```r fviz_pca_ind(res.pca, axes = c(1,2), col.ind = Donnees$Couleur, legend.title = "Couleur") ``` 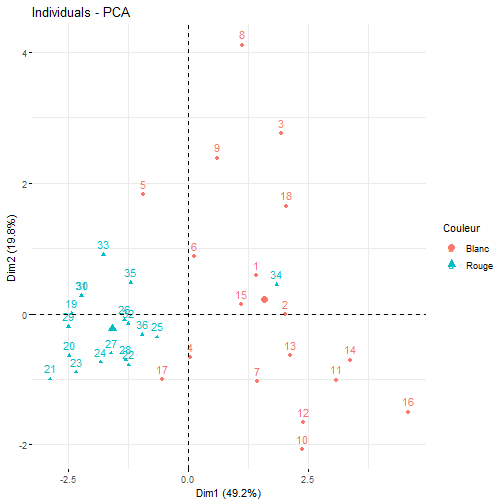 En revanche, l'effet `Origine` n'est pas présent sur ces deux premières composantes principales. ```r fviz_pca_ind(res.pca, axes = c(1,2), col.ind = Donnees$Origine, legend.title = "Origine") ``` 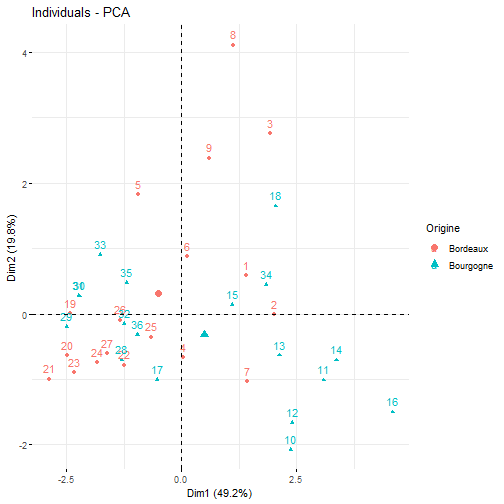 8. Quelles sont les vins les plus acides ? :Corrigé {#answer_ACP_vins8, toggle=collapse, title-display=show} 8. Comme cela a été vu sur le cercle des corrélations, la variable `AcTot` contribue positivement à la première composante principale. Ainsi, les vins les plus acides sont ceux situés à droite du graphique des individus : ce sont donc les vins blancs. :suite ACP {#ACP, toggle=collapse} [Choix de la métrique](caps_13_2_acp_metrique.html) [Calcul et visualisation de la matrice de corrélation](caps_13_3_acp_matrice_correlation.html) [Mise en place de l'analyse en composantes principales](caps_13_3bis_acp_mise_en_place_acp.html) [Choix du nombre d'axes pour l'interprétation](caps_13_4_acp_valeurs_propres.html) [Analyse du cercle des corrélations](caps_13_5_acp_cercle_correlation.html) [Analyse du graphique des individus](caps_13_6_acp_graphique_individus.html) [Exercice bilan](caps_13_7_acp_exercice_bilan.html)