Begin'R
Les statistiques avec R
Navigation
[Retour au sommaire]
## Croiser deux variables qualitatives :Objectifs Croiser deux variables qualitatives à l'aide de tableaux et de graphiques. :Remarque : Besoin de quelques rappels pour l'importation et la préparation du jeu de données? {#rq_preparation_donnees_graphiques_de_base, toggle=collapse, title-display=show} Les deux jeux de données utilisés dans les exemples et exercices sont les données `Melons` et `Vins`. Les liens ci-dessous permettent de télécharger les fichiers de données, de visionner une vidéo expliquant la description associée et d'obtenir les lignes de code pour importer le jeu de données sur R. | Jeu de données | Excel | CSV | Présentation | Commande R | Explication | |-----------------|--------|-------------|----------------|------------|-------------| | Données Melons | [](donnees/DonneesMelons.xlsx) | [](donnees/DonneesMelons.csv) | [](video/DonneesMelons.html) | [Importer le jeu de données](#ligne_code_importation_melons) | [Préparation du jeu de données Melons](#explication_preparation_importation_melons) | | Donneées Vins | [](donnees/DonneesVins.xlsx) | [](donnees/DonneesVins.csv) | [](video/DonneesVins.html) | [Importer le jeu de données](#ligne_code_importation_vins) | [Préparation du jeu de données Vins](#explication_preparation_importation_vins) | :Exemple {#ligne_code_importation_vins, toggle=popup} ```r Vins <- read.csv2("DonneesVins.csv", header = TRUE, stringsAsFactors = TRUE) ``` :Exemple {#explication_preparation_importation_vins, toggle=popup} Ici, pas de difficulté particulière pour l'importation des données "Vins" : ```r Vins <- read.csv2("DonneesVins.csv", header = TRUE, stringsAsFactors = TRUE) str(Vins) ``` ``` ## 'data.frame': 36 obs. of 11 variables: ## $ Origine : Factor w/ 2 levels "Bordeaux","Bourgogne": 1 1 1 1 1 1 1 1 1 2 ... ## $ Couleur : Factor w/ 2 levels "Blanc","Rouge": 1 1 1 1 1 1 1 1 1 1 ... ## $ Libelle : int 1 2 3 4 5 6 7 8 9 10 ... ## $ Alcool : num 12 11.5 14.6 10.5 14 13.2 11.2 15.4 13.4 11.4 ... ## $ pH : num 2.84 3.1 2.96 3.1 3.29 2.94 2.91 3.43 3.35 2.9 ... ## $ AcTot : int 89 97 99 72 76 83 95 86 76 103 ... ## $ Tartrique: num 21.1 26.4 20.7 29.7 22.3 24.6 39.4 14.1 18.9 50 ... ## $ Malique : num 21 34.2 21.8 4.2 9.3 9.4 14.5 28.8 23 18 ... ## $ Citrique : num 4.3 3.9 8.1 3.6 4.7 4.1 4.2 8.5 6.4 2.8 ... ## $ Acetique : num 16.9 9.9 19.7 11.9 20.1 19.7 19.4 15 14.4 14.4 ... ## $ Lactique : num 9.3 16 11.2 14.4 21.6 16.8 10.5 12.6 10.5 8.5 ... ``` Les variables sont reconnues selon leur nature. En particulier, les variables qualitatives `Origine` et `Couleur` sont reconnues comme telles car leurs modalités ne sont pas des nombres mais bien des chaînes de caractères. Seule la variable `Libelle` n'est pas reconnue comme une variable qualitative, puisqu'il s'agit du numéro d'individu. Elle peut toutefois être laissée en l'état. :Exemple {#ligne_code_importation_melons, toggle=popup} ```r Melons <- read.csv2("DonneesMelons.csv", header = TRUE, stringsAsFactors = TRUE) Melons <- transform(Melons, Creneau = as.ordered(Creneau), Couverture = as.factor(Couverture)) quatre_melons <- subset(Melons, Variete=='Cezanne'|Variete=='Fidji'|Variete=='Hugo'|Variete=='Manta') quatre_melons$Variete <- droplevels(quatre_melons$Variete) ``` :Exemple {#explication_preparation_importation_melons, toggle=popup} Dans un premier temps, [importer le jeu de données melons sur R Studio](caps_2_3_importation_CSV.html). ```r Melons <- read.csv2("DonneesMelons.csv", header = TRUE, stringsAsFactors = TRUE) Melons <- transform(Melons, Creneau = as.ordered(Creneau), Couverture = as.factor(Couverture)) ``` Pour ne pas alourdir les tableaux et représentations à venir, seules quatre variétés de melons sont considérées dans la suite : `Cezanne`, `Fidji`, `Hugo` et `Manta`. Pour cela, l'extraction peut être effectuée à l'aide de la fonction **`subset()`** : ```r quatre_melons <- subset(Melons, Variete=='Cezanne'|Variete=='Fidji'|Variete=='Hugo'|Variete=='Manta') levels(quatre_melons$Variete) ``` ``` ## [1] "Anasta" "Bastille" "Cezanne" "Escrito" "Fidji" "Heliobel" ## [7] "Hugo" "Indola" "Manta" "Mehari" "Metis" "Theo" ``` Après sélection des quatre variétés, le jeu de données garde la trace des anciennes variétés. La fonction **`droplevels()`** permet de "nettoyer" le jeu de données en éliminant les modalités non utilisées : ```r quatre_melons$Variete <- droplevels(quatre_melons$Variete) levels(quatre_melons$Variete) ``` ``` ## [1] "Cezanne" "Fidji" "Hugo" "Manta" ``` Désormais, les données sont accessibles via la variable `quatre_melons`, définie sur R comme un objet de type `data.frame`. ### Le tableau de contingence :Construire un tableau de contingence Il est possible de regrouper les données relatives à deux variables qualitatives sous la forme d’un tableau d’effectifs ou de fréquences. On parle de **tableau de contingence**. La réalisation d'un tableau de contingence sur R se fait à l'aide de la commande `table()`. :Exemple {#tableau_contingence,toggle=collapse} Pour le jeu de données `quatre_melons`, les variables `Variete` (en colonnes) et `Couverture` (en lignes) peuvent se croiser de la façon suivante : ```r tabCont=table(quatre_melons$Couverture,quatre_melons$Variete) print(tabCont) ``` ``` ## ## Cezanne Fidji Hugo Manta ## 1 17 5 0 16 ## 3 8 3 1 12 ## 5 0 2 11 2 ``` :Compléments : rajouter des sommes en lignes et en colonnes {#Sommes, toggle=collapse} Il est possible de rajouter les sommes en lignes et en colonnes, ainsi que le total général. ```r addmargins(tabCont) ``` ``` ## ## Cezanne Fidji Hugo Manta Sum ## 1 17 5 0 16 38 ## 3 8 3 1 12 24 ## 5 0 2 11 2 15 ## Sum 25 10 12 30 77 ``` :Exercice : construction d'un tableau de contingence {#exo_contingence, toggle=collapse} A partir du jeu de données `quatre_melons`, établir le tableau de contingence des variables relatives à la variété et au créneau de plantation (variables `Variete` et `Creneau`). :Corrigé : voir la réponse... {#Reponse_exo_contingence, toggle=collapse} On applique la commande `table()` pour construire le tableau de contingence : ```r creneau_vs_variete=table(quatre_melons$Creneau,quatre_melons$Variete) print(creneau_vs_variete) ``` ``` ## ## Cezanne Fidji Hugo Manta ## 1 14 4 3 13 ## 2 3 2 0 5 ## 3 8 3 1 8 ## 5 0 1 4 4 ## 6 0 0 4 0 ``` :Remarque : valeurs manquantes {#useNA, toggle=collapse} Il est possible de rendre compte des valeurs manquantes (aucune ici) dans le tableau de contingence en utilisant l'argument `useNA='always'` : ```r tabCont=table(quatre_melons$Couverture,quatre_melons$Variete,useNA='always') print(tabCont) ``` ``` ## ## Cezanne Fidji Hugo Manta <NA> ## 1 17 5 0 16 0 ## 3 8 3 1 12 0 ## 5 0 2 11 2 0 ## <NA> 0 0 0 0 0 ``` ### Normalisation du tableau de contingence :Calculer des pourcentages globaux, en lignes ou en colonnes Afin de remplacer les effectifs par des pourcentages, le tableau de contingence peut être normalisé à l'aide de la fonction `prop.table()` de 3 façons différentes : | Rôle | Commande R | Exemple | |:----------------------:|:--------------------:|:--------------------:| |Pourcentages globaux | `prop.table()` |[ ici ](#exemple_pourcentages_globaux)| |Pourcentages en lignes | `prop.table( , margin=1)` |[ ici ](#exemple_pourcentages_en_lignes)| |Pourcentages en colonnes| `prop.table( , margin=2)` |[ ici ](#exemple_pourcentages_en_colonnes)| :Exemple {#exemple_pourcentages_globaux, toggle=popup} La normalisation se fait ici par rapport à l’effectif total. Les fréquences relatives sont des pourcentages présentant un couple de modalités. L'utilisation de la commande `prop.table()` sur le tableau de contingence `tabCont` calculé plus haut permet d'obtenir les fréquences relatives : ```r Props=prop.table(tabCont) print(Props) ``` ``` ## ## Cezanne Fidji Hugo Manta <NA> ## 1 0.22077922 0.06493506 0.00000000 0.20779221 0.00000000 ## 3 0.10389610 0.03896104 0.01298701 0.15584416 0.00000000 ## 5 0.00000000 0.02597403 0.14285714 0.02597403 0.00000000 ## <NA> 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 ``` :Compléments : rajouter des pourcentages marginaux {#Marges, toggle=collapse} Il est possible, pour faciliter la lecture du tableau, de rajouter des pourcentages marginaux, ainsi que le total général , et d'afficher l'ensemble des valeurs entre 0 et 100. ```r Props2=addmargins(Props) Props2=round(100*Props2,1) print(Props2) ``` ``` ## ## Cezanne Fidji Hugo Manta <NA> Sum ## 1 22.1 6.5 0.0 20.8 0.0 49.4 ## 3 10.4 3.9 1.3 15.6 0.0 31.2 ## 5 0.0 2.6 14.3 2.6 0.0 19.5 ## <NA> 0.0 0.0 0.0 0.0 0.0 0.0 ## Sum 32.5 13.0 15.6 39.0 0.0 100.0 ``` :Exemple {#exemple_pourcentages_en_lignes, toggle=popup} L'utilisation de l'argument `margin=1` permet d'obtenir les pourcentages par rapport aux marges en lignes : ```r PropLig=prop.table(tabCont,margin=1) print(PropLig) ``` ``` ## ## Cezanne Fidji Hugo Manta <NA> ## 1 0.44736842 0.13157895 0.00000000 0.42105263 0.00000000 ## 3 0.33333333 0.12500000 0.04166667 0.50000000 0.00000000 ## 5 0.00000000 0.13333333 0.73333333 0.13333333 0.00000000 ## <NA> ``` :Compléments : rajouter des pourcentages marginaux {#MargesL, toggle=collapse} Il est possible, pour faciliter la lecture du tableau, de rajouter des pourcentages marginaux, et d'afficher l'ensemble des valeurs entre 0 et 100. ```r tabCont2=addmargins(tabCont,1) PropL2=prop.table(tabCont2,margin=1) PropsL2=addmargins(PropL2,2) PropsL2=round(100*PropsL2,1) print(PropsL2) ``` ``` ## ## Cezanne Fidji Hugo Manta <NA> Sum ## 1 44.7 13.2 0.0 42.1 0.0 100.0 ## 3 33.3 12.5 4.2 50.0 0.0 100.0 ## 5 0.0 13.3 73.3 13.3 0.0 100.0 ## <NA> ## Sum 32.5 13.0 15.6 39.0 0.0 100.0 ``` :Exemple {#exemple_pourcentages_en_colonnes, toggle=popup} L'utilisation de l'argument `margin=2` permet d'obtenir les pourcentages par rapport aux marges en colonnes : ```r PropCol=prop.table(tabCont,margin=2) print(PropCol) ``` ``` ## ## Cezanne Fidji Hugo Manta <NA> ## 1 0.68000000 0.50000000 0.00000000 0.53333333 ## 3 0.32000000 0.30000000 0.08333333 0.40000000 ## 5 0.00000000 0.20000000 0.91666667 0.06666667 ## <NA> 0.00000000 0.00000000 0.00000000 0.00000000 ``` :Compléments : rajouter des pourcentages marginaux {#MargesC, toggle=collapse} Il est possible, pour faciliter la lecture du tableau, de rajouter des pourcentages marginaux, et d'afficher l'ensemble des valeurs entre 0 et 100. ```r tabCont3=addmargins(tabCont,2) PropsC2=prop.table(tabCont3,margin=2) PropsC2=addmargins(PropsC2,1) PropsC2=round(100*PropsC2,1) print(PropsC2) ``` ``` ## ## Cezanne Fidji Hugo Manta <NA> Sum ## 1 68.0 50.0 0.0 53.3 49.4 ## 3 32.0 30.0 8.3 40.0 31.2 ## 5 0.0 20.0 91.7 6.7 19.5 ## <NA> 0.0 0.0 0.0 0.0 0.0 ## Sum 100.0 100.0 100.0 100.0 100.0 ``` :Exercice : Calcul de fréquences relatives {#exo_prop, toggle=collapse} Établir le tableau de fréquences relatives fournissant, pour chaque variété, les proportions des différents créneaux de plantation (variables `Variete` et `Creneau`). :Corrigé {#Reponse_exo_prop, toggle=collapse} On applique la commande `prop.table()` au tableau de contingence en lui indiquant de procéder par colonne (`margin=2`) : ```r creneau_vs_variete=table(quatre_melons$Creneau,quatre_melons$Variete) creneau_vs_variete_col=prop.table(creneau_vs_variete,margin=2) print(creneau_vs_variete_col) ``` ``` ## ## Cezanne Fidji Hugo Manta ## 1 0.56000000 0.40000000 0.25000000 0.43333333 ## 2 0.12000000 0.20000000 0.00000000 0.16666667 ## 3 0.32000000 0.30000000 0.08333333 0.26666667 ## 5 0.00000000 0.10000000 0.33333333 0.13333333 ## 6 0.00000000 0.00000000 0.33333333 0.00000000 ``` ### Graphiques associés :Croiser deux variables qualitatives avec des graphiques en barres La relation entre deux variables qualitatives peut également être représentée graphiquement. Parmi les graphiques existant, les diagrammes en barres se prêtent facilement à la représentation des tableaux de contingence mais d'autres graphiques sont parfois utilisés. Voici quelques exemples : | Rôle | Commande R | Exemple | |:---------------------:|:--------------------:|:--------------------:| |Diagramme en barres stratifiées | `barplot()` | [ ici ](#exemple_barplot_strat)| |Diagramme en barres empilées | `barplot()`| [ ici ](#exemple_barplot_empile)| |Diagramme en barres empilées 100% | `barplot()` | [ ici ](#exemple_barplot_empile_100)| |Diagramme en mosaïque | `mosaicplot()`| [ ici ](#exemple_mosaicplot)| :Exemple {#exemple_barplot_strat, toggle=popup} Comme dans le cas de série statistique univariée, il est possible dans le cas de série statistique bivariée de construire un diagramme en barres. On utilise pour cela les fréquences (ou les effectifs) disponibles dans le tableau de contingence. Le graphique ainsi construit est appelé **diagramme en barres stratifiées**. Si l'on considère les variables `Variete` et `Couverture`. Le diagramme s'obtient en appliquant la commande `barplot()` au tableau de contingence `tabCont` précédemment construit : ```r barplot(tabCont,legend=rownames(tabCont),beside=TRUE) ``` 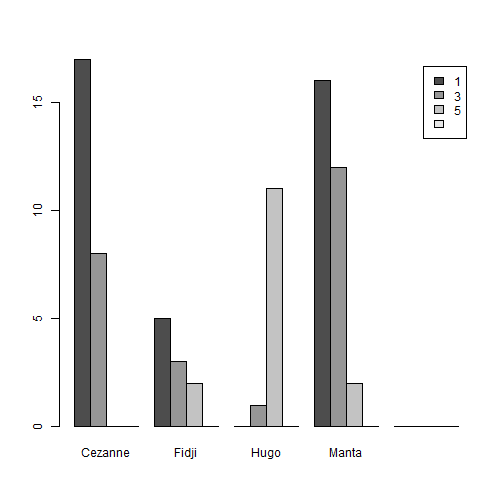 Les fréquences des différentes variétés, stratifiées par type de couverture, sont représentées par des barres disposées côte à côte. Il ne s'agit pas de l'option par défaut de `barplot()`, puisqu'elle nécessite l'utilisation de l'argument `beside=TRUE`. Notons ici l'affichage d'une légende grâce à l'argument `legend` auquel on affecte les noms de lignes du tableau de contingence `tabCont`. :Exemple {#exemple_barplot_empile, toggle=popup} Le diagramme en barres empilées est une variante du diagramme en barres : ```r barplot(tabCont,xlab="Variétés",legend=rownames(tabCont)) ``` 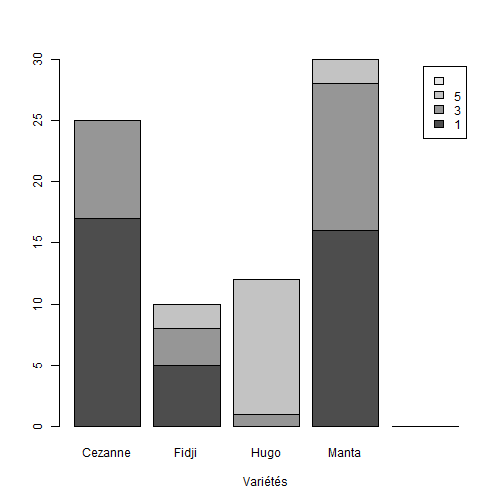 Les barres relatives aux différentes couvertures sont ici empilées. C'est le comportement par défaut de la commande `barplot()`, correspondant à l'argument `beside=FALSE`. :Exemple {#exemple_barplot_empile_100, toggle=popup} Cette dernière variante est sans doute la plus simple à interpréter. C'est toujours la commande `barplot()` qui est utilisée, mais sur les pourcentages en colonnes contenus dans le tableau `PropCol` calculé précédemment : ```r barplot(PropCol,xlab="Variétés",legend=rownames(tabCont)) ``` 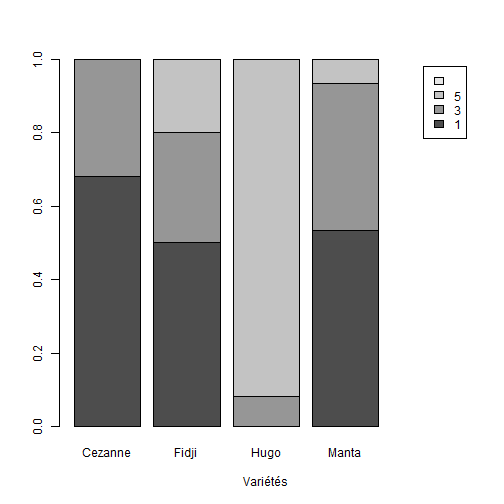 :Exemple {#exemple_mosaicplot, toggle=popup} Le diagramme en **mosaïque** permet d'avoir un aspect visuel des tableaux de contingence, ce qui constitue une alternative intéressante aux diagrammes en barres. Il est ici construit à partir du tableau de contingence transposé (les variétés figurent en lignes). ```r tabContBis=table(quatre_melons$Variete,quatre_melons$Couverture) print(tabContBis) ``` ``` ## ## 1 3 5 ## Cezanne 17 8 0 ## Fidji 5 3 2 ## Hugo 0 1 11 ## Manta 16 12 2 ``` ```r mosaicplot(tabContBis) ``` 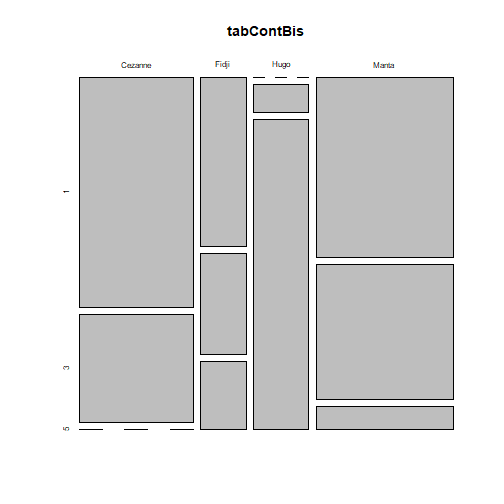 Les colonnes (relatives aux variétés) sont toutes de même hauteur mais les largeurs (et donc les aires) sont proportionnelles aux fréquences des variétés. :Compléments : Améliorer un diagramme en mosaïque {#complement_mosaic, toggle=collapse} Voici comment rajouter un titre général, des titres aux axes, des couleurs et une légende... ```r mosaicplot(tabContBis,main="Variétés et couvertures",xlab="Variétés",ylab="Couverture",col=terrain.colors(3)) legend(x='topright',fill=terrain.colors(3),legend=rownames(tabCont),title="Couverture") ``` 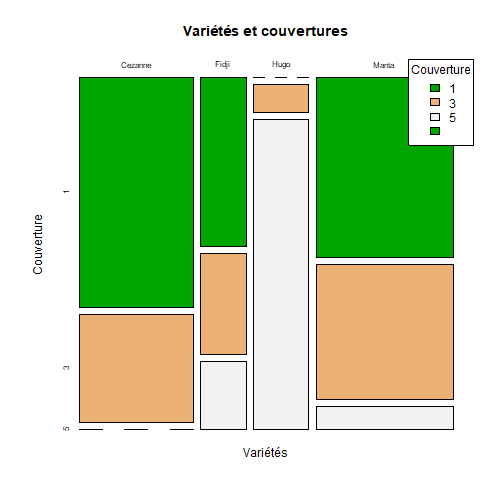 :Exercice : Tracer un diagramme en barres {#exo_barplot, toggle=collapse} Pour les variables `Variete` et `Creneau`, écrire les commandes permettant de construire le graphique suivant : 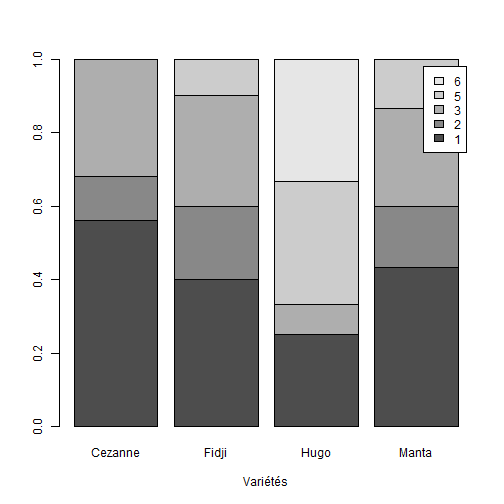 :Corrigé {#corrige_exo_barplot, toggle=collapse} Disposant déjà du tableau de contingence et du tableau des pourcentages en colonnes, le tracé du diagramme en barres est immédiat : ```r creneau_vs_variete=table(quatre_melons$Creneau,quatre_melons$Variete) creneau_vs_variete_col=prop.table(creneau_vs_variete,margin=2) barplot(creneau_vs_variete_col,xlab="Variétés",legend=rownames(creneau_vs_variete_col)) ``` 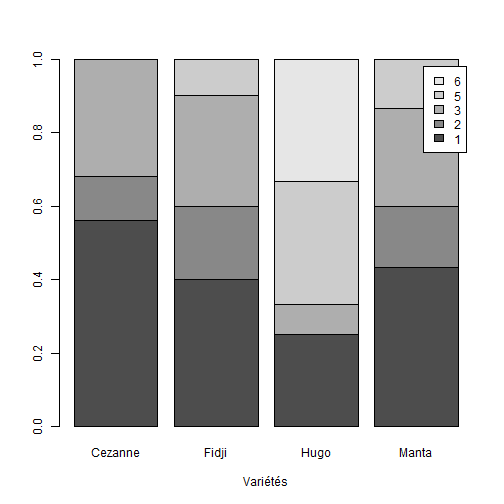 :Suite des Statistiques descriptives bivariées {#biv, toggle=collapse, title-display=hidden} [Téléchargement et présentation des données](caps_4_1_objectifs&donnees.html) [Croiser deux variables qualitatives](caps_4_2_quali_quali.html) [Croiser une variables quantitative et une variable qualitative](caps_4_3_quali_quanti.html) [Croiser deux variables quantitatives](caps_4_4_quanti_quanti.html)