Begin'R
Les statistiques avec R
Navigation
[Retour au sommaire]
## Croiser une variable qualitative et une variable quantitative :Objectifs Croiser une variable qualitative et une variable quantitative à l'aide résumés numériques et graphiques. :Remarque : Besoin de quelques rappels pour l'importation et la préparation du jeu de données? {#rq_preparation_donnees_graphiques_de_base, toggle=collapse, title-display=show} Les deux jeux de données utilisés dans les exemples et exercices sont les données `Melons` et `Vins`. Les liens ci-dessous permettent de télécharger les fichiers de données, de visionner une vidéo expliquant la description associée et d'obtenir les lignes de code pour importer le jeu de données sur R. | Jeu de données | Excel | CSV | Présentation | Commande R | Explication | |-----------------|--------|-------------|----------------|------------|-------------| | Données Melons | [](donnees/DonneesMelons.xlsx) | [](donnees/DonneesMelons.csv) | [](video/DonneesMelons.html) | [Importer le jeu de données](#ligne_code_importation_melons) | [Préparation du jeu de données Melons](#explication_preparation_importation_melons) | | Donneées Vins | [](donnees/DonneesVins.xlsx) | [](donnees/DonneesVins.csv) | [](video/DonneesVins.html) | [Importer le jeu de données](#ligne_code_importation_vins) | [Préparation du jeu de données Vins](#explication_preparation_importation_vins) | :Exemple {#ligne_code_importation_vins, toggle=popup} ```r Vins <- read.csv2("DonneesVins.csv", header = TRUE, stringsAsFactors = TRUE) ``` :Exemple {#explication_preparation_importation_vins, toggle=popup} Ici, pas de difficulté particulière pour l'importation des données "Vins" : ```r Vins <- read.csv2("DonneesVins.csv", header = TRUE, stringsAsFactors = TRUE) str(Vins) ``` ``` ## 'data.frame': 36 obs. of 11 variables: ## $ Origine : Factor w/ 2 levels "Bordeaux","Bourgogne": 1 1 1 1 1 1 1 1 1 2 ... ## $ Couleur : Factor w/ 2 levels "Blanc","Rouge": 1 1 1 1 1 1 1 1 1 1 ... ## $ Libelle : int 1 2 3 4 5 6 7 8 9 10 ... ## $ Alcool : num 12 11.5 14.6 10.5 14 13.2 11.2 15.4 13.4 11.4 ... ## $ pH : num 2.84 3.1 2.96 3.1 3.29 2.94 2.91 3.43 3.35 2.9 ... ## $ AcTot : int 89 97 99 72 76 83 95 86 76 103 ... ## $ Tartrique: num 21.1 26.4 20.7 29.7 22.3 24.6 39.4 14.1 18.9 50 ... ## $ Malique : num 21 34.2 21.8 4.2 9.3 9.4 14.5 28.8 23 18 ... ## $ Citrique : num 4.3 3.9 8.1 3.6 4.7 4.1 4.2 8.5 6.4 2.8 ... ## $ Acetique : num 16.9 9.9 19.7 11.9 20.1 19.7 19.4 15 14.4 14.4 ... ## $ Lactique : num 9.3 16 11.2 14.4 21.6 16.8 10.5 12.6 10.5 8.5 ... ``` Les variables sont reconnues selon leur nature. En particulier, les variables qualitatives `Origine` et `Couleur` sont reconnues comme telles car leurs modalités ne sont pas des nombres mais bien des chaînes de caractères. Seule la variable `Libelle` n'est pas reconnue comme une variable qualitative, puisqu'il s'agit du numéro d'individu. Elle peut toutefois être laissée en l'état. :Exemple {#ligne_code_importation_melons, toggle=popup} ```r Melons <- read.csv2("DonneesMelons.csv", header = TRUE, stringsAsFactors = TRUE) Melons <- transform(Melons, Creneau = as.ordered(Creneau), Couverture = as.factor(Couverture)) quatre_melons <- subset(Melons, Variete=='Cezanne'|Variete=='Fidji'|Variete=='Hugo'|Variete=='Manta') quatre_melons$Variete <- droplevels(quatre_melons$Variete) ``` :Exemple {#explication_preparation_importation_melons, toggle=popup} Dans un premier temps, [importer le jeu de données melons sur R Studio](caps_2_3_importation_CSV.html). ```r Melons <- read.csv2("DonneesMelons.csv", header = TRUE, stringsAsFactors = TRUE) Melons <- transform(Melons, Creneau = as.ordered(Creneau), Couverture = as.factor(Couverture)) ``` Pour ne pas alourdir les tableaux et représentations à venir, seules quatre variétés de melons sont considérées dans la suite : `Cezanne`, `Fidji`, `Hugo` et `Manta`. Pour cela, l'extraction peut être effectuée à l'aide de la fonction **`subset()`** : ```r quatre_melons <- subset(Melons, Variete=='Cezanne'|Variete=='Fidji'|Variete=='Hugo'|Variete=='Manta') levels(quatre_melons$Variete) ``` ``` ## [1] "Anasta" "Bastille" "Cezanne" "Escrito" "Fidji" "Heliobel" ## [7] "Hugo" "Indola" "Manta" "Mehari" "Metis" "Theo" ``` Après sélection des quatre variétés, le jeu de données garde la trace des anciennes variétés. La fonction **`droplevels()`** permet de "nettoyer" le jeu de données en éliminant les modalités non utilisées : ```r quatre_melons$Variete <- droplevels(quatre_melons$Variete) levels(quatre_melons$Variete) ``` ``` ## [1] "Cezanne" "Fidji" "Hugo" "Manta" ``` Désormais, les données sont accessibles via la variable `quatre_melons`, définie sur R comme un objet de type `data.frame`. Différentes pistes sont envisageables, fondées sur la représentation d'histogrammes, de statistiques gaussiennes (moyennes et écarts-types) ou de statistiques d'ordre (quantiles). ### Comparaison d'histogrammes :Exemple : Comparer les histogrammes des poids de quatre variétés {#hist_stratifie, toggle=collapse} Afin de comparer les poids des melons selon les variétés, il est possible de réaliser quatre histogrammes, un par variété. Il faut pour cela répartir les données en quatre sous-ensembles à l'aide de la commande `subset()` : ```r Cezanne=subset(quatre_melons,Variete=='Cezanne') Fidji=subset(quatre_melons,Variete=='Fidji') Hugo=subset(quatre_melons,Variete=='Hugo') Manta=subset(quatre_melons,Variete=='Manta') ``` Les histogrammes sont alors affichés en quatre graphiques distincts : ```r par(mfrow=c(2,2)) hist(Cezanne$Poids,breaks=seq(600,1400,100)) hist(Fidji$Poids,breaks=seq(600,1400,100)) hist(Hugo$Poids,breaks=seq(600,1400,100)) hist(Manta$Poids,breaks=seq(600,1400,100)) ``` 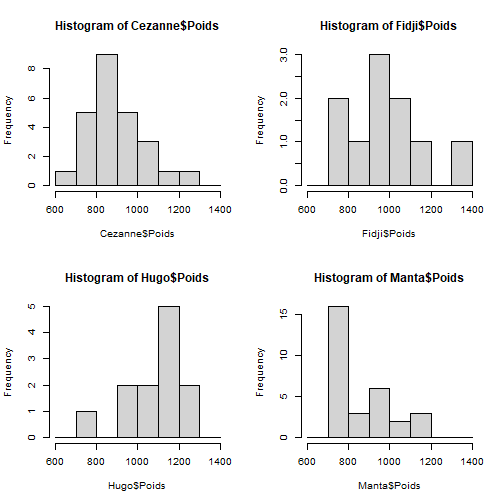 :Remarque : + les limites de classes sont ici imposées à l'aide de l'argument `breaks=seq(600,1400,100)`. Sans cela, la commande `hist()` pourrait réaliser un découpage différent pour chaque type de couverture, ce qui compliquerait leur comparaison. + l'utilisation de l'instruction `par(mfrow=c(2,2))` permet d'organiser la fenêtre graphique en 2 lignes et 2 colonnes. On revient ensuite à une fenêtre graphique standard en appliquant l'instruction `par(mfrow=c(1,1))` : ```r par(mfrow=c(1,1)) ``` :Exercice : Comparaison d'histogrammes {#exo_3hist, toggle=collapse} On considère les variables `Rdt` et `Couverture` du jeu de données `quatre_melons`. Écrire les commandes permettant de produire un graphique représentant les histogrammes du rendement des melons sous chaque mode de couverture (1, 3 ou 5). :Corrigé {#Reponse_exo_3hist, toggle=collapse} La première étape consiste à définir les sous-ensembles de données relatifs aux trois modes de couverture : ```r Couv1=subset(quatre_melons,Couverture=='1') Couv3=subset(quatre_melons,Couverture=='3') Couv5=subset(quatre_melons,Couverture=='5') ``` Les histogrammes sont ensuite tracés en gardant toujours les mêmes définitions de classes (soit 0 à 450 par pas de 50 tonnes par hectare) : ```r par(mfrow=c(1,3)) hist(Couv1$Rdt,breaks=seq(0,450,50)) hist(Couv3$Rdt,breaks=seq(0,450,50)) hist(Couv5$Rdt,breaks=seq(0,450,50)) ``` 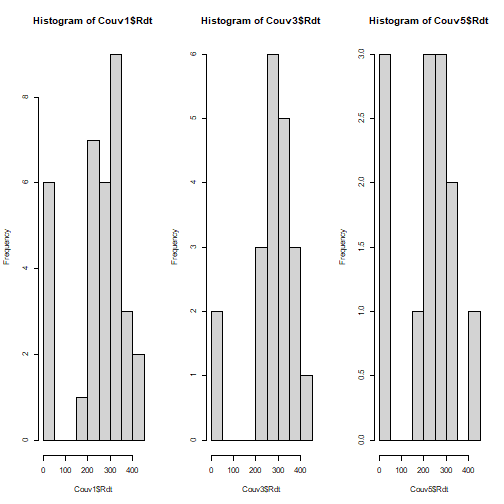 Pour finir, la fenêtre graphique peut être rétablie à son état initial : ```r par(mfrow=c(1,1)) ``` ### Moyennes et écart-types Il est assez courant, afin de résumer ces distributions, d'utiliser certaines statistiques comme la moyenne et l'écart-type. :Exemple : Représenter des moyennes par un diagramme en barres {#moyennes_en_barres, toggle=collapse} Les poids moyens des quatre variétés du jeu de données `quatre_melons` peuvent être calculées à l'aide de la commande `tapply()` : ```r tab_moy=tapply(quatre_melons$Poids,INDEX=quatre_melons$Variete,FUN=mean,na.rm=TRUE) print(tab_moy) ``` ``` ## Cezanne Fidji Hugo Manta ## 894.44 985.50 1083.00 866.60 ``` ```r barplot(tab_moy) ``` 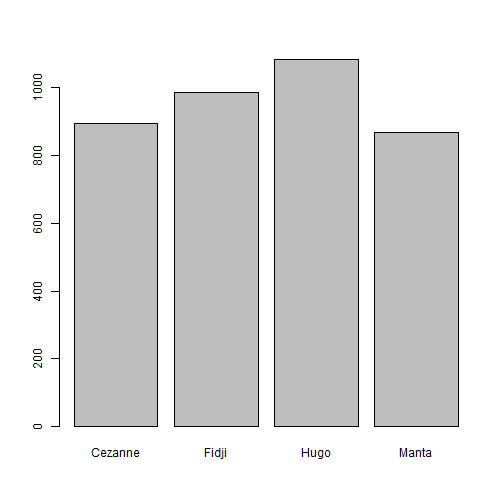 La commande `tapply()` permet d'appliquer une commande (définie par l'argument `FUN`) à une variable (passée en premier argument) pour chaque modalité d'une variable qualitative (fournie par l'argument `INDEX`). Cette commande renvoie un objet de type `data.frame` qui est ici affiché, puis utilisé directement par la commande `barplot()`. L'argument `na.rm=TRUE` permet d'ignorer les valeurs manquantes dans le calcul réalisé par `tapply()`. :Remarque : de l'intérêt des barres d'erreur {#BarresErreur, toggle=collapse} La représentation des seules moyennes s'avère généralement peu satisfaisante car trop synthétique. Afin de compléter le graphique, il convient généralement de rajouter des barres d'erreur représentant, par exemple, les écarts-types au sein de chaque catégorie. :Compléments : ajouter des barres d'erreur à un graphique des moyennes {#compl_barres_erreurs, toggle=collapse} Il est possible d'ajouter aux barres représentant les moyennes, des barres d'erreur dont les limites inférieures et supérieures correspondent aux moyennes respectivement plus ou moins la valeur des écarts-types. Les écarts-types peuvent être estimés à l'aide de la commande **`sd()`**. La commande `tapply()` permet de répéter le calcul pour les différentes variétés. ```r tab_moy = tapply(quatre_melons$Poids,INDEX = quatre_melons$Variete,FUN = mean,na.rm=TRUE) tab_et = tapply(quatre_melons$Poids,INDEX = quatre_melons$Variete,FUN = sd,na.rm=TRUE) tab_et ``` ``` ## Cezanne Fidji Hugo Manta ## 135.3080 166.6122 135.4789 144.3997 ``` Les limites inférieures et supérieures des barres sont alors obtenues comme ceci : ```r limite_inf = tab_moy - tab_et limite_sup = tab_moy + tab_et ``` Il reste à tracer tout cela, en commençant par le graphique en barres : ```r posx=barplot(tab_moy,ylim=c(0,1400)) arrows(x0 = posx, y0 = tab_moy - tab_et, x1 = posx, y1 = tab_moy + tab_et, angle=90, code=3,length=0.1) ``` 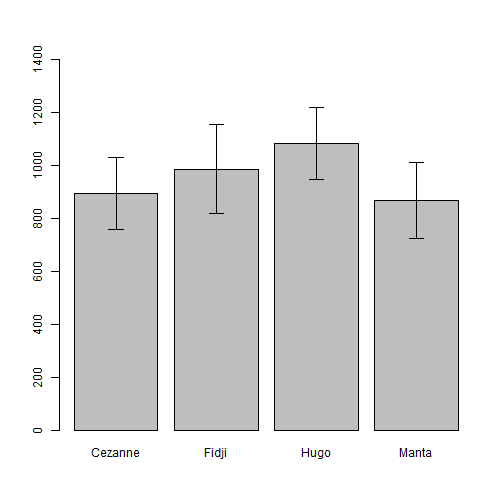 Quelques explications : + à la première ligne, les positions X (abscisses) des barres représentant les moyennes sont récupérées dans une variable `posx`. L'ordonnée maximale du graphique est fixée à 1400 afin de pouvoir visualiser les barres d'erreur dans leur totalité. + à la deuxième ligne, la commande `arrows()` permet de tracer les barres proprement dites. On lui indique les positions de début et de fin (x puis y) des flèches à tracer. ### Collections de box-plots (ou boîtes à moustaches) Une solution alternative, très séduisante, consiste à réaliser une comparaison de box-plots. Cela se fait de façon totalement automatique à l'aide de la commande `boxplot()`. Pour ce qui est des arguments, deux possibilités existent : + la première consiste à fournir à la commande toutes les séries que l'ont veut représenter, + la seconde consiste à utiliser une **formule**. :Exemple : Comparer plusieurs box-plots {#boxplot_collection, toggle=collapse} Pour représenter le poids des melons en fonction de la variété, la première option se traduit par l'instruction suivante : ```r boxplot(Cezanne$Poids,Fidji$Poids,Hugo$Poids,Manta$Poids,names=c("Cezanne","Fidji","Hugo","Manta")) ``` Il est ici nécessaire de préciser les libellés des quatre séries (à l'aide de l'argument `names`). La seconde écriture est bien plus simple : ```r boxplot(quatre_melons$Poids~quatre_melons$Variete) ``` La formule `quatre_melons$Poids~quatre_melons$Variete` se lit "Poids **en fonction** de la variété". Cette seconde méthode s'avère souvent plus pratique. Elle identifie automatiquement les niveaux de la variable en abscisse, sans qu'il soit nécessaire de les lister. Le résultat est le même dans les deux cas : 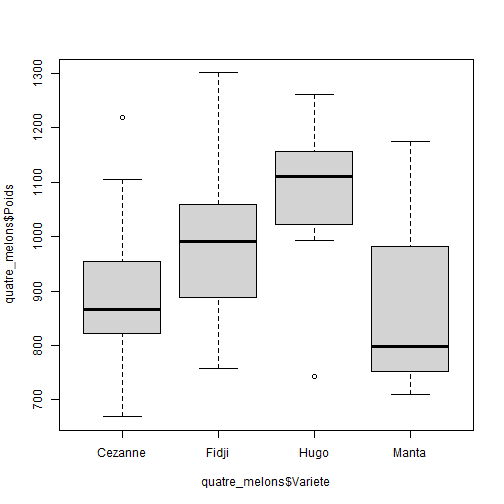 :Exercice : Comparer plusieurs box-plots {#exo_boxplot_collection, toggle=collapse} On souhaite comparer les rendements (`Rdt`) des melons obtenus sous les trois modes de couverture (`Couverture`) du jeu de données `quatre_melons`. Écrire les commandes permettant d'obtenir le graphique suivant : 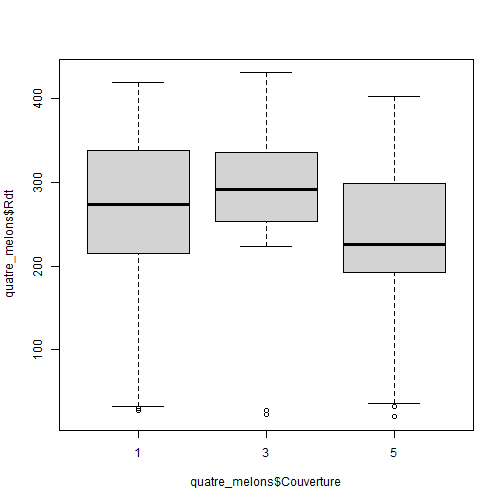 :Corrigé {#reponse_boxplot_collection, toggle=collapse} Deux solutions sont possibles à l'aide de la commande `boxplot()` dont celle basée sur une formule : ```r boxplot(quatre_melons$Rdt~quatre_melons$Couverture) ``` 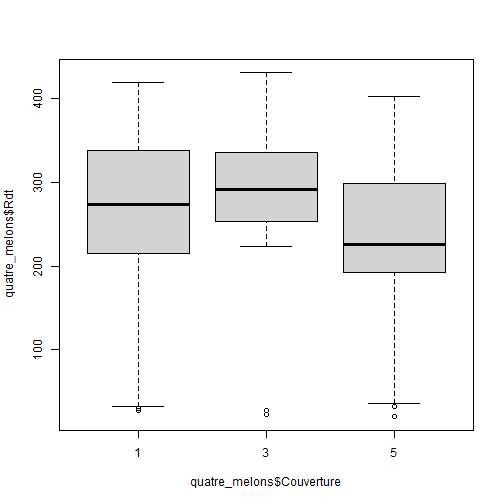 :Suite des Statistiques descriptives bivariées {#biv, toggle=collapse, title-display=hidden} [Téléchargement et présentation des données](caps_4_1_objectifs&donnees.html) [Croiser deux variables qualitatives](caps_4_2_quali_quali.html) [Croiser une variables quantitative et une variable qualitative](caps_4_3_quali_quanti.html) [Croiser deux variables quantitatives](caps_4_4_quanti_quanti.html)