Begin'R
Les statistiques avec R
Navigation
[Retour au sommaire]
## Croiser deux variables quantitatives :Objectifs Croiser deux variables quantitatives à l'aide de graphiques. :Remarque : Besoin de quelques rappels pour l'importation et la préparation du jeu de données? {#rq_preparation_donnees_graphiques_de_base, toggle=collapse, title-display=show} Les deux jeux de données utilisés dans les exemples et exercices sont les données `Melons` et `Vins`. Les liens ci-dessous permettent de télécharger les fichiers de données, de visionner une vidéo expliquant la description associée et d'obtenir les lignes de code pour importer le jeu de données sur R. | Jeu de données | Excel | CSV | Présentation | Commande R | Explication | |-----------------|--------|-------------|----------------|------------|-------------| | Données Melons | [](donnees/DonneesMelons.xlsx) | [](donnees/DonneesMelons.csv) | [](video/DonneesMelons.html) | [Importer le jeu de données](#ligne_code_importation_melons) | [Préparation du jeu de données Melons](#explication_preparation_importation_melons) | | Donneées Vins | [](donnees/DonneesVins.xlsx) | [](donnees/DonneesVins.csv) | [](video/DonneesVins.html) | [Importer le jeu de données](#ligne_code_importation_vins) | [Préparation du jeu de données Vins](#explication_preparation_importation_vins) | :Exemple {#ligne_code_importation_vins, toggle=popup} ```r Vins <- read.csv2("DonneesVins.csv", header = TRUE, stringsAsFactors = TRUE) ``` :Exemple {#explication_preparation_importation_vins, toggle=popup} Ici, pas de difficulté particulière pour l'importation des données "Vins" : ```r Vins <- read.csv2("DonneesVins.csv", header = TRUE, stringsAsFactors = TRUE) str(Vins) ``` ``` ## 'data.frame': 36 obs. of 11 variables: ## $ Origine : Factor w/ 2 levels "Bordeaux","Bourgogne": 1 1 1 1 1 1 1 1 1 2 ... ## $ Couleur : Factor w/ 2 levels "Blanc","Rouge": 1 1 1 1 1 1 1 1 1 1 ... ## $ Libelle : int 1 2 3 4 5 6 7 8 9 10 ... ## $ Alcool : num 12 11.5 14.6 10.5 14 13.2 11.2 15.4 13.4 11.4 ... ## $ pH : num 2.84 3.1 2.96 3.1 3.29 2.94 2.91 3.43 3.35 2.9 ... ## $ AcTot : int 89 97 99 72 76 83 95 86 76 103 ... ## $ Tartrique: num 21.1 26.4 20.7 29.7 22.3 24.6 39.4 14.1 18.9 50 ... ## $ Malique : num 21 34.2 21.8 4.2 9.3 9.4 14.5 28.8 23 18 ... ## $ Citrique : num 4.3 3.9 8.1 3.6 4.7 4.1 4.2 8.5 6.4 2.8 ... ## $ Acetique : num 16.9 9.9 19.7 11.9 20.1 19.7 19.4 15 14.4 14.4 ... ## $ Lactique : num 9.3 16 11.2 14.4 21.6 16.8 10.5 12.6 10.5 8.5 ... ``` Les variables sont reconnues selon leur nature. En particulier, les variables qualitatives `Origine` et `Couleur` sont reconnues comme telles car leurs modalités ne sont pas des nombres mais bien des chaînes de caractères. Seule la variable `Libelle` n'est pas reconnue comme une variable qualitative, puisqu'il s'agit du numéro d'individu. Elle peut toutefois être laissée en l'état. :Exemple {#ligne_code_importation_melons, toggle=popup} ```r Melons <- read.csv2("DonneesMelons.csv", header = TRUE, stringsAsFactors = TRUE) Melons <- transform(Melons, Creneau = as.ordered(Creneau), Couverture = as.factor(Couverture)) quatre_melons <- subset(Melons, Variete=='Cezanne'|Variete=='Fidji'|Variete=='Hugo'|Variete=='Manta') quatre_melons$Variete <- droplevels(quatre_melons$Variete) ``` :Exemple {#explication_preparation_importation_melons, toggle=popup} Dans un premier temps, [importer le jeu de données melons sur R Studio](caps_2_3_importation_csv.html). ```r Melons <- read.csv2("DonneesMelons.csv", header = TRUE, stringsAsFactors = TRUE) Melons <- transform(Melons, Creneau = as.ordered(Creneau), Couverture = as.factor(Couverture)) ``` Pour ne pas alourdir les tableaux et représentations à venir, seules quatre variétés de melons sont considérées dans la suite : `Cezanne`, `Fidji`, `Hugo` et `Manta`. Pour cela, l'extraction peut être effectuée à l'aide de la fonction **`subset()`** : ```r quatre_melons <- subset(Melons, Variete=='Cezanne'|Variete=='Fidji'|Variete=='Hugo'|Variete=='Manta') levels(quatre_melons$Variete) ``` ``` ## [1] "Anasta" "Bastille" "Cezanne" "Escrito" "Fidji" "Heliobel" ## [7] "Hugo" "Indola" "Manta" "Mehari" "Metis" "Theo" ``` Après sélection des quatre variétés, le jeu de données garde la trace des anciennes variétés. La fonction **`droplevels()`** permet de "nettoyer" le jeu de données en éliminant les modalités non utilisées : ```r quatre_melons$Variete <- droplevels(quatre_melons$Variete) levels(quatre_melons$Variete) ``` ``` ## [1] "Cezanne" "Fidji" "Hugo" "Manta" ``` Désormais, les données sont accessibles via la variable `quatre_melons`, définie sur R comme un objet de type `data.frame`. ### Le nuage de points C'est une représentation classique. Une des variables est représentée en abscisse, l'autre en ordonnée. Chaque point se définit par ses coordonnées `(x,y)`, `x` étant donnée par la variable en abscisse, `y` par la variable en ordonnée. :Exemple : Représentation conjointe des variables `Acide malique` et `Acidité totale` {#scatter_plot, toggle=collapse} On considère le jeu de données `Vins` et le couple de variables **Acide malique** et **Acidité totale** (resp. `Malique` et `AcTot`). Le nuage de points (**Scatter plot** en anglais) est obtenu à l'aide de la commande `plot()` : ```r plot(Vins$Malique,Vins$AcTot) ``` 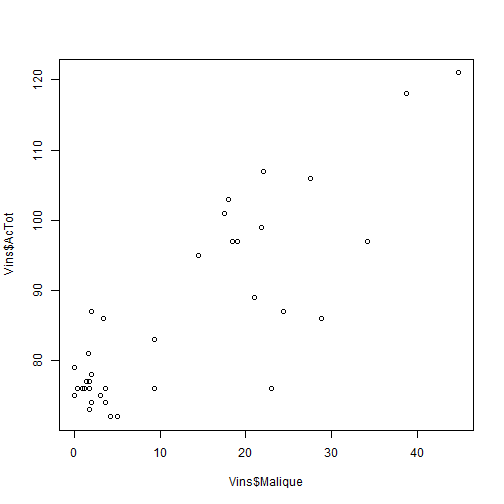 :Exercice : Deux nuages de points {#exo_scatter_plot, toggle=collapse} Afin d'approfondir l'analyse de la relation entre **Acide malique** et **Acidité totale**, représenter séparément, par deux nuages de points, les vins rouges et les vins blancs. :Corrigé {#Reponse_exo_scatter_plot, toggle=collapse} Les nuages de points sont obtenus après séparations des vins rouges et des vins blancs à l'aide de la commande `subset` : ```r Rouges=subset(Vins,Couleur=="Rouge") Blancs=subset(Vins,Couleur=="Blanc") par(mfrow=c(1,2)) plot(Rouges$Malique,Rouges$AcTot,main="Vins rouges",xlim=c(0,50),ylim=c(70,120)) plot(Blancs$Malique,Blancs$AcTot,main="Vins blancs",xlim=c(0,50),ylim=c(70,120)) ``` 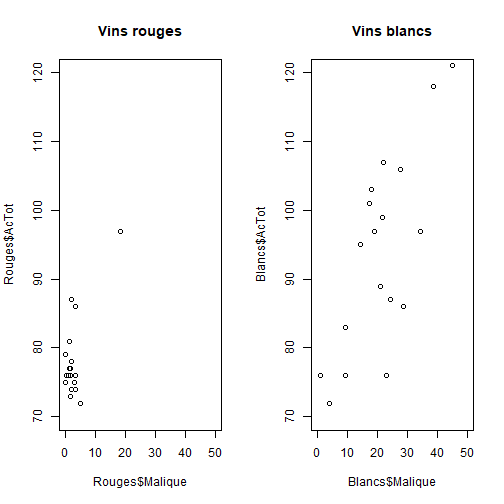 A noter : Les mêmes échelles d'axes sont utilisées pour les deux graphiques afin de faciliter la comparaison. :Compléments : Tracer un **nuage de points stratifié** {#nuage_stratifie, toggle=collapse} Il est possible, en paramétrant correctement la commande `plot()`, de réaliser **un nuage de points stratifié**. La relation **Activité totale versus Acide malique** peut ainsi être représentée à l'aide d'un seul et même graphique distinguant vins rouges et vins blancs : ```r par(mfrow=c(1,1)) plot(Vins$Malique,Vins$AcTot,col=Vins$Couleur,main="Acidité totale vs. Acide malique") legend("bottomright",legend=levels(Vins$Couleur),col=1:2,pch=1) ``` 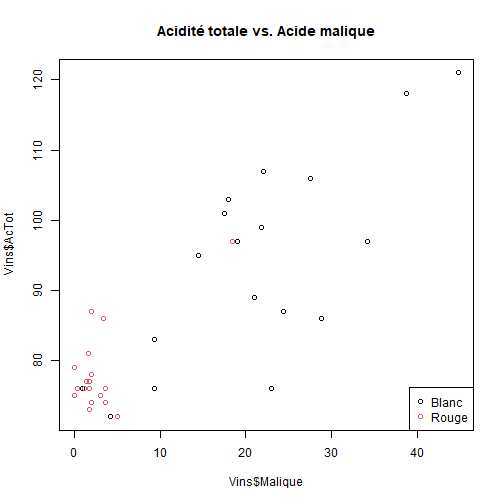 Cette représentation est bien entendu plus compacte que celle utilisant deux graphiques. Elle appelle cependant l'utilisation d'une légende que l'on peut afficher grâce à l'argument `legend`. ### Mesures de corrélation Les deux principales mesures de la liaison entre deux variables quantitatives sont la **covariance** et le **coefficient de corrélation linéaire de Pearson**. |Rôle | Commande R | Remarque| Exemple | |:------------------|:-----------------------|:------:|:------:| |Covariance | `cov()` | [ici](#detail_cov) | [ici](#exemple_cov)| |Coefficient de corrélation | `cor()` | [ici](#detail_cor) | [ici](#exemple_cor)| :Aide {#detail_cov, toggle=popup} La covariance est un indicateur du sens de la liaison entre deux variables : On dit qu’elles sont **corrélées** si la covariance est positive, **anti-corrélées** si la covariance est négative, **décorrélées** si la covariance est nulle. :Remarque {#rq_unite_covariance} L’unité de la covariance est obtenue par produit des unités des deux variables. Elle peut prendre des valeurs a priori quelconques entre $-\infty$ et $+\infty$ (en fonction des variables utilisées et de leurs unités). Il est donc difficile, à partir de la valeur prise par la covariance, de déterminer si deux variables sont fortement ou faiblement corrélées ou anti-corrélées. Le **coefficient de corrélation de Pearson** donne une réponse à ce problème. :Exemple {#exemple_cov, toggle=popup} La commande `cov()` est utilisée pour calculer la covariance des variables `Acide malique` et `Acidité totale` du jeu de données `DonneesVins` : ```r cov(Vins$Malique,Vins$AcTot) ``` ``` ## [1] 140.7051 ``` :Aide {#detail_cor, toggle=popup} Le coefficient de corrélation linéaire de Pearson (ou Bravais Pearson) est obtenu en normalisant la covariance par les écarts-types des deux variables. Il est ainsi borné entre -1 et 1. Les variables sont corrélées si le coefficient de corrélation est proche de 1, anti-corrélées s'il est proche de -1, décorrélées s'il est proche de zéro. Il se calcule à l'aide de la commande `cor()`. :Exemple {#exemple_cor, toggle=popup} La commande `cor()` est employée pour calculer le coefficient de corrélation des variables `Acide malique` et `Acidité totale` du jeu de données `DonneesVins` : ```r cor(Vins$Malique,Vins$AcTot) ``` ``` ## [1] 0.8392382 ``` :Exercice : Calculer des coefficients de corrélation {#exo_cor, toggle=collapse} Calculer le coefficient de corrélation entre les variables `Acide Malique` et `Acidité totale` sur les vins blancs et les vins rouges. :Corrigé {reponse_cor, toggle=collapse} Sur les vins blancs : ```r Blancs=subset(Vins,Couleur=="Blanc") cor(Blancs$Malique,Blancs$AcTot) ``` ``` ## [1] 0.751959 ``` Sur les vins rouges : ```r Rouges=subset(Vins,Couleur=="Rouge") cor(Rouges$Malique,Rouges$AcTot) ``` ``` ## [1] 0.6980095 ``` :Compléments : Coefficients de corrélation non paramétriques {#add_spearman_kendall, toggle=collapse} Voici deux exemples de coefficients de corrélation non paramétriques : Le coefficient de Spearman est basé sur une transformation en rangs et le coefficient de Kendall basé sur une mesure très simple de la liaison entre deux variables. Ils sont tous les deux normalisés entre -1 et 1. | Rôle | Commande R | Exemple | |:------------------|:-----------------------|:------:| |Spearman | `cor(... ,method="spearman")` | [ici](#exemple_spearman)| |Kendall | `cor(... ,method="kendall")` | [ici](#exemple_kendall)| :Exemple {#exemple_spearman, toggle=popup} La commande `cor()` avec l'option `method="spearman"` permet de calculer le coefficient de Spearman pour les variables `Acide malique` et `Acidité totale` : ```r cor(Rouges$Malique,Rouges$AcTot,method="spearman") ``` ``` ## [1] -0.04438648 ``` :Exemple {#exemple_kendall, toggle=popup} La commande `cor()` avec l'option `method="kendall"` permet de calculer le coefficient de Kendall pour les variables `Acide malique` et `Acidité totale` : ```r cor(Rouges$Malique,Rouges$AcTot,method="kendall") ``` ``` ## [1] -0.01384091 ``` :Suite des Statistiques descriptives bivariées {#biv, toggle=collapse, title-display=hidden} [Téléchargement et présentation des données](caps_4_1_objectifs&donnees.html) [Croiser deux variables qualitatives](caps_4_2_quali_quali.html) [Croiser une variables quantitative et une variable qualitative](caps_4_3_quali_quanti.html) [Croiser deux variables quantitatives](caps_4_4_quanti_quanti.html)