Begin'R
Les statistiques avec R
Navigation
[Retour au sommaire]
# Autour de la loi normale :Objectifs * Utiliser les préfixes [p,q,r,d] pour la loi normale Une loi normale $\mathcal{N}(\mu;\sigma)$ est caractérisée par l'espérance $\mu$ et l'écart-type $\sigma$ qui correspondent respectivement aux arguments `mean` et `sd` des fonctions R ayant pour suffixe `norm`. :Calcul de probabilité (préfixe p) {#remarque_p, toggle=collapse} La fonction **`pnorm(q, mean, sd)`** renvoie la probabilité $\mathbb{P}\left(X \leq q \right)$, c'est-à-dire l'image de `q` par la **fonction de répartition** de la loi normale dont l'argument `mean` est associé à l'espérance et `sd` à l'écart-type. :Exemple {#example_pnorm} Soit $X$ une variable distribuée selon la loi normale d'espérance $\mu=100$ et d'écart-type $\sigma = 5$. Les probabilités $\mathbb{P}\left(X \leq 105 \right)$ et $\mathbb{P}\left(X \geq 110 \right)$ se calculent respectivement par : ```r pnorm(q = 105, mean = 100, sd = 5) ``` ``` ## [1] 0.8413447 ``` ```r 1 - pnorm(q = 110, mean = 100, sd = 5) ``` ``` ## [1] 0.02275013 ``` :Calcul d'un quantile (préfixe q) {#remarque_q, toggle=collapse} La fonction **`qnorm(p, mean, sd)`** calcule le quantile d'ordre `p` où `p` correspond à une probabilité. :Exemple {#example_qnorm} Soit $X$ une variable distribuée selon la loi normale d'espérance $\mu=100$ et d'écart-type $\sigma = 5$. Le quantile $x$ d'ordre $0,975$ tel que $\mathbb{P}\left(X \leq x \right)= 0,975$ est donné par : ```r qnorm(p = 0.975, mean = 100, sd = 5) ``` ``` ## [1] 109.7998 ``` :Génération de données (préfixe r) {#remarque_r, toggle=collapse} La fonction **`rnorm(n, mean, sd)`** renvoie, sous la forme d'un vecteur, un **échantillon** de $n$ valeurs issues de la loi normale dont l'argument `mean` est associé à l'espérance et `sd` à l'écart-type. :Exemple {#example_rnorm} Un échantillon de $10$ valeurs issues de la loi normale d'espérance $\mu=100$ et d'écart-type $\sigma = 5$ s'obtient ainsi : ```r rnorm(n = 10, mean = 100, sd = 5) ``` ``` ## [1] 107.80727 103.62639 102.08337 96.92964 103.59662 101.87131 102.05046 ## [8] 108.71397 98.26573 102.90324 ``` :Densité de probabilité (préfixe d) {#remarque_d, toggle=collapse} Enfin, la fonction **`dnorm(x, mean, sd)`** est la fonction de **densité de probabilité**, de la loi normale d'espérance `mean` et d'écart-type `sd`, associée aux éléments du vecteur `x` fourni en premier argument. :Exemple : Représentation de la fonction de densité d'une loi normale {#example_courbenorm} Pour représenter la fonction de densité de la loi normale d'espérance $\mu=100$ et d'écart-type $\sigma = 5$, il faut d'abord créer un vecteur $x$, grâce à la fonction `seq()`, décrivant par exemple l'intervalle $\left[85 ; 115\right]$ avec un pas de $0,2$ et ensuite utiliser ensuite la fonction `dnorm()` ```r x = seq(from = 85, to = 115, by = 0.2) plot(x, dnorm(x, mean = 100, sd = 5), type = "l", col = "black", lwd = 2, main = "Densité de la loi N(100;5)") ``` 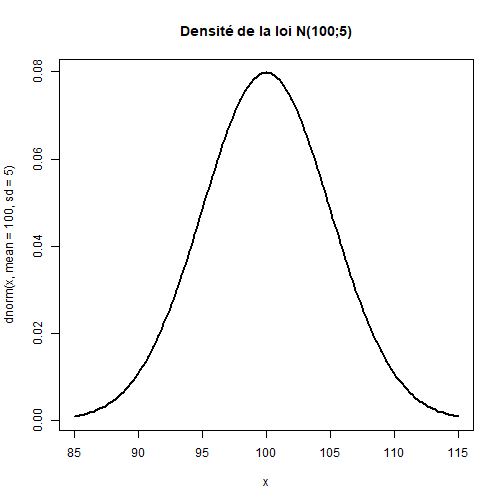 :Exercice : Application avec la loi normale d'espérance $\mu=12$ et d'écart-type $\sigma =3$ {#exercise_normal, toggle = collapse} Soit $X$ une variable aléatoire distribuée selon une loi normale d'espérance $\mu=12$ et d'écart-type $\sigma =3$. 1. Déterminer $\mathbb{P}\left(X \leq 10 \right)$. 2. Calculer le quantile $x$ d'ordre $0,9$. 3. Produire un échantillon de 5 valeurs de $X$. 4. Représenter la fonction de répartition de $X$ sur l'intervalle $\left[0 ; 20\right]$. :Corrigé {#answer_normal, toggle=collapse, title-display=show} 1. Déterminer $\mathbb{P}\left(X \leq 10 \right)$. ```r pnorm(10, mean = 12, sd = 3) ``` ``` ## [1] 0.2524925 ``` 2. Calculer le quantile $x$ d'ordre $0,9$. ```r qnorm(p = 0.9, mean = 12, sd = 3) ``` ``` ## [1] 15.84465 ``` 3. Produire un échantillon de 5 valeurs de $X$. ```r rnorm(n = 5, mean = 12, sd = 3) ``` ``` ## [1] 10.298564 12.761004 8.127495 11.646095 13.493394 ``` 4. Représenter la fonction de répartition de $X$ sur l'intervalle $\left[0 ; 20\right]$. ```r x = seq(from = 0, to = 20, by = 0.5) plot(x, pnorm(x, mean = 12, sd = 3), type = "l", col = "blue", lwd = 2, main = "Fonction de répartition de la loi N(12;3)") ``` 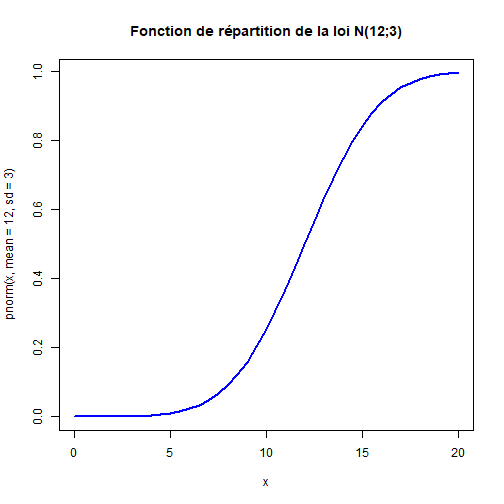 :Suite de Calculs de probabilités {#proba, toggle=collapse, title-display=hidden} [Loi normale](caps_6_1_loi_normale.html) [Loi binomiale](caps_6_4_loi_binomiale.html) [Lois continues](caps_6_2_lois_continues.html) [Lois discrètes](caps_6_5_lois_discretes.html) [Normalité : graphiques quantile-quantile](caps_6_3_normalite_graphique_quantile_quantile.html) [Exercice bilan](caps_6_6_exercice_bilan.html)