Begin'R
Les statistiques avec R
Navigation
[Retour au sommaire]
# Autour de la loi binomiale :Objectifs * Utiliser les préfixes [p,q,r,d] pour la loi binomiale Une loi binomiale $\mathcal{B}(n;p)$ est caractérisée par la valeur de l'effectif $n$ et la probabilité de succès $p$ qui correspondent respectivement aux arguments `size` et `prob` des fonctions R ayant pour suffixe `binom`. :Calcul de probabilité (préfixe p) {#remarque_pbinom, toggle=collapse} La fonction **`pbinom(q, size, prob)`** renvoie la probabilité $\mathbb{P}\left(X \leq q \right)$, c'est-à-dire l'image de `q` par la **fonction de répartition** de la loi binomiale dont l'argument `size` est associé à la valeur de l'effectif $n$ et `prob` à la probabilité de succès $p$. :Exemple {#example_pbinom} Soit $X$ une variable distribuée selon la loi binomiale de paramètres $n = 20$ et $p = 0.3$. Les probabilités $\mathbb{P}\left(X \leq 10 \right)$ et $\mathbb{P}\left(X \geq 15 \right)$ se calculent respectivement par : ```r pbinom(q = 10, size = 20, prob = 0.3) ``` ``` ## [1] 0.9828552 ``` ```r 1 - pbinom(q = 14, size = 20, prob = 0.3) ``` ``` ## [1] 4.294002e-05 ``` :Calcul d'un quantile (préfixe q) {#remarque_qbinom, toggle=collapse} La fonction **`qbinom(p, size, prob)`** calcule le quantile d'ordre `p` où `p` correspond à une probabilité. :Exemple {#example_qbinom} Soit $X$ une variable distribuée selon la loi binomiale de paramètres $n = 20$ et $p = 0.3$. Le quantile $x$ d'ordre $0,975$ tel que $\mathbb{P}\left(X \leq x \right)= 0,975$ est donné par : ```r qbinom(p = 0.975, size = 20, prob = 0.3) ``` ``` ## [1] 10 ``` :Génération de données (préfixe r) {#remarque_rbinom, toggle=collapse} La fonction **`rbinom(n, size, prob)`** renvoie, sous la forme d'un vecteur, un **échantillon** de $n$ valeurs issues de la loi binomiale de paramètres $n$ et $p$. :Exemple {#example_rbinom} Un échantillon de $10$ valeurs issues de la loi binomiale de paramètres $n=20$ et $p = 0.3$ s'obtient ainsi : ```r rbinom(n = 10, size = 20, p = 0.3) ``` ``` ## [1] 9 6 7 6 7 8 5 8 7 5 ``` :Densité de probabilité (préfixe d) {#remarque_dbinom, toggle=collapse} Enfin, la fonction **`dbinom(x, size, prob)`** renvoie la probabilité $\mathbb{P}(X = x)$, de la loi binomiale de paramètres $n$ et $p$. :Exemple : {#example_dbinom} Soit $X$ une variable aléatoire distribuée selon la loi binomiale $\mathcal{B}(20;0.3)$. $\mathbb{P}(X = 2)$ s'obtient par la commande ```r dbinom(2, size = 20, prob = 0.3) ``` ``` ## [1] 0.02784587 ``` :Exercice : Autour de la loi binomiale $\mathcal{B}(8;0,5)$ {#exoBinomiale, toggle = collapse} Soit $X$ une variable de loi binomiale $\mathcal{B}\left(8;0,5 \right)$. Déterminer : 1. $\mathbb{P}\left(X = 2 \right)$. 2. $\mathbb{P}\left(X \leq 2 \right)$. 3. $\mathbb{P}\left(X \geq 2 \right)$. 4. Représenter la loi de $X$. :Corrigé {#repBinomiale, toggle=collapse, title-display=show} 1. $P(X=2)$ correspond à : ```r dbinom(x = 2, size = 8, prob = 0.5) ``` ``` ## [1] 0.109375 ``` 2. $P\left(X \leq 2 \right)$ correspond à : ```r pbinom(2, size = 8, prob = 0.5) ``` ``` ## [1] 0.1445313 ``` 3. $P\left(X \geq 2 \right) = 1 - P\left(X < 2 \right) = 1 - P\left(X \leq 1 \right)$. Ainsi, $P\left(X \geq 2 \right)$ correspond à : ```r 1 - pbinom(1, size = 8, prob = 0.5) ``` ``` ## [1] 0.9648438 ``` 4. Représentation graphique ```r x = seq(from = 0, to = 8, by = 1) barplot(dbinom(x, size = 8, prob = 0.5), col = "red", names.arg = x, xlab = "k", ylab = "P(X = k)", main = "Représentation de la loi B(8;0,5)") ``` 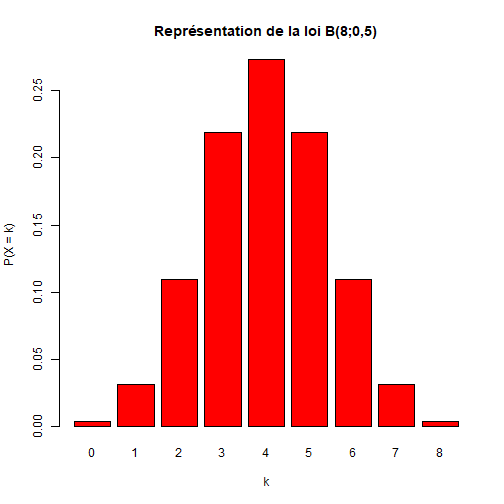 :Suite de Calculs de probabilités {#proba, toggle=collapse, title-display=hidden} [Loi normale](caps_6_1_loi_normale.html) [Loi binomiale](caps_6_4_loi_binomiale.html) [Lois continues](caps_6_2_lois_continues.html) [Lois discrètes](caps_6_5_lois_discretes.html) [Normalité : graphiques quantile-quantile](caps_6_3_normalite_graphique_quantile_quantile.html) [Exercice bilan](caps_6_6_exercice_bilan.html)