Begin'R

Navigation

# Exercice bilan
    
    
    :Objectifs
        
        * Évaluer ses compétences sur l'utilisation de lois de probabilités.
    
    
    :Exercice : Autour de la loi binomiale $\mathcal{B}(50;0,3)$ {#binom_normal}
        
        
        1. Simuler un vecteur `simu` de 1000 valeurs d'une variable $X$ de loi binomiale de paramètres $n = 50$  et $p = 0,3$.
        
        2. On note : `a = mean(simu)`  et `b = sd(simu)`. Représenter en bleu la densité de loi normale d'espérance `a` et d'écart-type `b`.
        
        3. Représenter en rouge la densité de la loi normale d'espérance $np$ et d'écart-type $\sqrt{np(1-p)} $.
        
        :Corrigé {#answerBinomNormal, toggle=collapse, title-display=show}
            
            
            ```r
                n = 50
                p = 0.3
                nbsimul = 1000
                x = seq(from = 0, to = 50, by = 0.1)
                simu = rbinom(n = nbsimul, size = n, prob = p )
                hist(simu, probability = TRUE, ylim = c(0,0.15), main = "Histogramme et courbes de fonctions de densité")
                lines(x, dnorm(x, mean = mean(simu), sd = sd(simu)), col = "blue")
                lines(x, dnorm(x, mean = n*p, sd = sqrt(n*p*(1-p))), col = "red")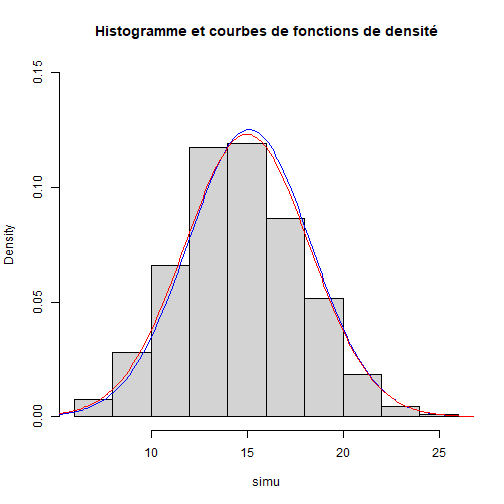
            ```
            
            ![plot of chunk C6-6-A](figure/C6-6-A-1.png)
            
:Suite de Calculs de probabilités {#proba, toggle=collapse, title-display=hidden}
    
    [Loi normale](caps_6_1_loi_normale.html)
    
    [Loi binomiale](caps_6_4_loi_binomiale.html)
    
    [Lois continues](caps_6_2_lois_continues.html)
    
    [Lois discrètes](caps_6_5_lois_discretes.html)
    
    [Normalité : graphiques quantile-quantile](caps_6_3_normalite_graphique_quantile_quantile.html)

[Exercice bilan](caps_6_6_exercice_bilan.html)