Begin'R
Les statistiques avec R
Navigation
[Retour au sommaire]
# Tests d'ajustement à une distribution théorique {#tests-ajustement-theo} :Objectifs * Mettre en place un test d'ajustement à une distribution théorique. | Rôle | Commande R | Arguments | Exemple | Exercice | |---------------------|-------------------------|---------------|--------------------------------------|------------------------------------------| | Distribution quelconque (variable qualitative) | `chisq.test()` | `x`, `p` | [ ici ](#exo_test_khideux_Adequation) | | | Distribution quelconque (variable quantitative) | `ks.test()` | `x`, `y`, ... | [ ici ](#ExeKolm) | | | Normalité (variable quantitative continue) | `shapiro.test()` | `x` | [ ici ](#ExeShapiro) | [ ici ](#ExoShapiro) | :Exemple {#ExeKolm, toggle=popup} On a observé la durée de vie, en semaines, de 10 composants électroniques. Les résultats obtenus sont les suivants : 187, 40, 15, 173, 9, 67, 107, 151, 131, 16 A l'aide d'un test de Kolmogorov-Smirnov, on souhaite tester l'hypothèse $\mathcal{H}_0$ selon laquelle la durée de vie des composants est distribuée suivant la loi exponentielle de paramètre $\dfrac{1}{100}$. ```r durees = c(187, 40, 15, 173, 9, 67, 107, 151, 131, 16) ks.test(x = durees, y = "pexp", 1/100) ``` ``` ## ## One-sample Kolmogorov-Smirnov test ## ## data: durees ## D = 0.15699, p-value = 0.9351 ## alternative hypothesis: two-sided ``` La probabilité est supérieure à 5 % (voisine de 0.935) donc, au vu de ces résultats, on ne peut pas rejeter l'hypothèse selon laquelle la durée de vie de ces composants est distribuée selon la loi exponentielle de paramètre $\dfrac{1}{100}$. :Remarque Le second argument de la fonction `ks.test()` est associé à la fonction de répartition de la loi de probabilité (préfixe `p` suivi du nom de la loi), les arguments suivants étant associés à chacun des paramètres caractérisant la loi "testée". Ainsi, pour tester l'hypothèse selon laquelle une variable suit la loi $\mathcal{N}(0;1)$, on utiliserait `ks.test(x, y = "pnorm", 0, 1)`. :Exemple {#ExeShapiro, toggle=popup} On considère les données issues de l'étude i-Share accessibles via les fichiers ci-dessous : | Jeu de données | Excel | CSV | |-----------------|--------|-------------| | DonneesIShare | [](donnees/DonneesIShare.xlsx) | [](donnees/DonneesIShare.csv) | On souhaite savoir si la distribution de la variable `malbouffe` chez les étudiants de sexe masculin et âgés de 20 ans est normale. ```r donnees <- read.csv2("DonneesIShare.csv", header = TRUE, stringsAsFactors = TRUE) # Extraction des étudiants masculins âgés de 20 ans donnees_G_20_ans <- subset(donnees, donnees$age == 20 & donnees$sexe == "G") # Mise en place du test de Shapiro shapiro.test(donnees_G_20_ans$malbouffe) ``` ``` ## ## Shapiro-Wilk normality test ## ## data: donnees_G_20_ans$malbouffe ## W = 0.98952, p-value = 0.366 ``` La valeur-$p$ associée au test est supérieure à 5%. On ne peut donc pas rejeter l'hypothèse $\mathcal{H}_0$ selon laquelle la variable `malbouffe` est distribuée normalement. :Compléments{#complements_subset_shapiro, toggle = collapse} Il est possible de réaliser les opérations d'extraction des individus et de mise en place du test de Shapiro en une seule ligne de code via l'utilisation du `which` : ```r shapiro.test(donnees$malbouffe[which(donnees$age == 20 & donnees$sexe == "G")]) ``` :Exemple {#exo_test_khideux_Adequation, toggle=popup} On effectue un croisement en génétique. En théorie, on devrait observer dans la descendance : 75% d'individus aux yeux marrons et 25% aux yeux bleus. On observe en réalité sur une génération de 40 individus : 32 individus aux yeux marrons et 8 aux yeux bleus. On met en place un test du Khi-deux à l'aide de la fonction `chisq.test()` pour savoir si ces observations sont conformes aux lois génétiques. Les arguments `x` et `p` sont associés respectivement aux effectifs observés (32 et 8) et à la loi de probabilité associée (0,75 et 0,25). Théoriquement, il y a 3/4 individus aux yeux marrons et 1/4 d'individus aux yeux bleus. ```r observations <- c(32, 8) Loi_proba <- c(0.75, 0.25) test <- chisq.test(x = observations, p = Loi_proba) test ``` ``` ## ## Chi-squared test for given probabilities ## ## data: observations ## X-squared = 0.53333, df = 1, p-value = 0.4652 ``` La valeur-$p$ est supérieure à 5 % (voisine de 0.465) donc, au vu de ces résultats, on ne peut pas conclure à une différence entre l’échantillon et la répartition théorique. :Exemple {#ExoShapiro, toggle = popup} On considère l'étude réalisée sur la composition de vins associée au fichier de données `DonneesVins.csv`. | Jeu de données | Excel | CSV | Présentation | |-----------------|--------|-------------|----------------| | DonneesVins | [](donnees/DonneesVins.xlsx) | [](donnees/DonneesVins.csv) | [](video/DonneesVins.html) | On s'intéresse plus particulièrement à la distribution de la variable `Alcool`. Nous cherchons à savoir si celle-ci est distribuée normalement. 1. Tracer un graphique quantile-quantile associé à cette variable. Émettre une hypothèse sur la distribution de cette variable. :Aide{toggle=collapse} La fonction permettant de représenter [le graphique quantile-quantile](caps_6_3_normalite_graphique_quantile_quantile.html) est `qqnorm()` 2. Effectuer un test statistique qui confirme ou rejette cette hypothèse puis conclure. :Corrigé {#rep_Shapiro, toggle=collapse, title-display=show} 1. La fonction permettant de représenter [le graphique quantile-quantile](caps_6_3_normalite_graphique_quantile_quantile.html) est `qqnorm()` ```r donnees <- read.csv2("DonneesVins.csv", header = TRUE, stringsAsFactors = TRUE) qqnorm(donnees$Alcool) qqline(donnees$Alcool, col = "red") ``` 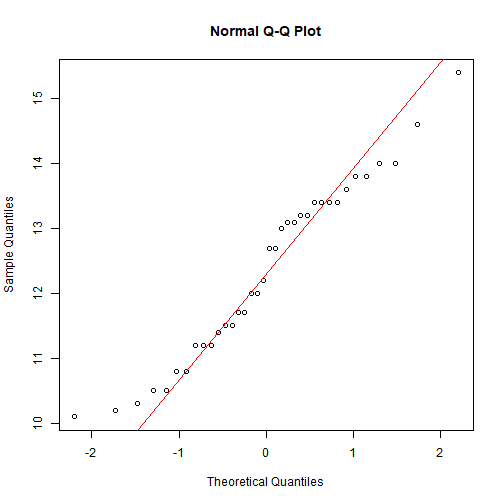 Les observations étant alignées sur la droite de Henry, l'hypothèse de normalité semble valide. 2. Pour vérifier la normalité d'une distribution observée, nous utilisons un test de Shapiro à l'aide de la fonction `shapiro.test()` ```r shapiro.test(donnees$Alcool) ``` ``` ## ## Shapiro-Wilk normality test ## ## data: donnees$Alcool ## W = 0.9594, p-value = 0.2059 ``` La valeur-$p$ associée au test est supérieure à 5%. Nous ne pouvons donc pas rejeter la normalité de la distribution de cette variable à partir de cet échantillon. :Suite des Tests {#tests, toggle=collapse, title-display=hidden} [Introduction : exemple du Khi-deux](caps_7_1_objectifs&intro_chi-deux.html) [Tests de conformité et intervalles de confiance](caps_7_2_conformite_para.html) [Tests d'ajustement à une distribution théorique](caps_7_3_conformite_distrib.html) [Tests paramétriques d'homogénéité](caps_7_4_homogeneite_para.html) [Tests non-paramétriques d'homogénéité](caps_7_5_homogeneite_non_para.html) [Tests d'indépendance de deux variables qualitatives](caps_7_6_indep.html) [Tests de corrélation de deux variables quantitatives](caps_7_7_corr.html) [Résumé](caps_7_8_resume.html)