Begin'R
Les statistiques avec R
Navigation
[Retour au sommaire]
# Régression linéaire multiple: mise en oeuvre :Objectifs * Mettre en oeuvre un modèle de régression linéaire multiple, entre une variable à expliquer quantitative et plusieurs variables explicatives quantitatives. :Remarque : Importation et préparation du jeu de données ? {#rq_preparation_donnees_regression, toggle=collapse, title-display=show} Dans les parties sur la régression linéaire, deux jeux de données sont employés. Le jeu de données `ozone`pour les exemples et le jeu de données `her`pour les exercices. | Jeu de données | Excel | CSV | Txt | Présentation du jeu de données| |-----------------|--------|-------------|----------------|-------------| | Ozone | [](donnees/Ozone.xlsx) | [](donnees/ozone.csv) | [](donnees/ozone.txt) |[ozone](#ozoneexp)| |her| |[](donnees/her.csv) | |[her](#herexp)| [Rappel : comment importer un jeu de données](caps_2_3_importation_csv.html) :Aide{#ozoneexp, toggle=popup, title-display=hidden} Un jeu de données sur la pollution d'ozone, issu d'une étude de surveillance de la qualité de l'air à Rennes pendant l'été 2001, est considéré. Dans cette partie, l'objectif est d'expliquer la pollution d'ozone `maxO3` (concentration en $\mu g /m^3$) d'un jour donné à l'aide de variables explicatives : * des variables de température T9, T12, T15 (les suffixes 9, 12 et 15 désignant respectivement des mesures prises à 9h, 12h et 15h, pour toutes les variables) ; * des variables de nébulosité Ne9, Ne12, Ne15 ; * des variables de vent Vx9, Vx12, Vx15 ; * la mesure du maximum de la concentration en ozone de la veille maxO3v. :Exemple Télécharger le fichier `ozone` et importer le jeu de données dans RStudio {#eximport} :Corrigé{#import, toggle=collapse} Le jeu de données sur la pollution d'ozone peut être importé à partir du fichier `ozone.csv` comme suit : ```r ozone <- read.csv2("donnees/ozone.csv", header = TRUE, stringsAsFactors = TRUE) ozone ``` ``` ## X maxO3 T9 T12 T15 Ne9 Ne12 Ne15 Vx9 Vx12 Vx15 maxO3v ## 1 20010601 87 15.6 18.5 18.4 4 4 8 0.6946 -1.7101 -0.6946 84 ## 2 20010602 82 17.0 18.4 17.7 5 5 7 -4.3301 -4.0000 -3.0000 87 ## 3 20010603 92 15.3 17.6 19.5 2 5 4 2.9544 1.8794 0.5209 82 ## 4 20010604 114 16.2 19.7 22.5 1 1 0 0.9848 0.3473 -0.1736 92 ## 5 20010605 94 17.4 20.5 20.4 8 8 7 -0.5000 -2.9544 -4.3301 114 ## 6 20010606 80 17.7 19.8 18.3 6 6 7 -5.6382 -5.0000 -6.0000 94 ## 7 20010607 79 16.8 15.6 14.9 7 8 8 -4.3301 -1.8794 -3.7588 80 ## 8 20010610 79 14.9 17.5 18.9 5 5 4 0.0000 -1.0419 -1.3892 99 ## 9 20010611 101 16.1 19.6 21.4 2 4 4 -0.7660 -1.0261 -2.2981 79 ## 10 20010612 106 18.3 21.9 22.9 5 6 8 1.2856 -2.2981 -3.9392 101 ## 11 20010613 101 17.3 19.3 20.2 7 7 3 -1.5000 -1.5000 -0.8682 106 ## 12 20010614 90 17.6 20.3 17.4 7 6 8 0.6946 -1.0419 -0.6946 101 ## 13 20010615 72 18.3 19.6 19.4 7 5 6 -0.8682 -2.7362 -6.8944 90 ## 14 20010616 70 17.1 18.2 18.0 7 7 7 -4.3301 -7.8785 -5.1962 72 ## 15 20010617 83 15.4 17.4 16.6 8 7 7 -4.3301 -2.0521 -3.0000 70 ## 16 20010618 88 15.9 19.1 21.5 6 5 4 0.5209 -2.9544 -1.0261 83 ## 17 20010620 145 21.0 24.6 26.9 0 1 1 -0.3420 -1.5321 -0.6840 121 ## 18 20010621 81 16.2 22.4 23.4 8 3 1 0.0000 0.3473 -2.5712 145 ## 19 20010622 121 19.7 24.2 26.9 2 1 0 1.5321 1.7321 2.0000 81 ## 20 20010623 146 23.6 28.6 28.4 1 1 2 1.0000 -1.9284 -1.2155 121 ## 21 20010624 121 20.4 25.2 27.7 1 0 0 0.0000 -0.5209 1.0261 146 ## 22 20010625 146 27.0 32.7 33.7 0 0 0 2.9544 6.5778 4.3301 121 ## 23 20010626 108 24.0 23.5 25.1 4 4 0 -2.5712 -3.8567 -4.6985 146 ## 24 20010627 83 19.7 22.9 24.8 7 6 6 -2.5981 -3.9392 -4.9240 108 ## 25 20010628 57 20.1 22.4 22.8 7 6 7 -5.6382 -3.8302 -4.5963 83 ## 26 20010629 81 19.6 25.1 27.2 3 4 4 -1.9284 -2.5712 -4.3301 57 ## 27 20010630 67 19.5 23.4 23.7 5 5 4 -1.5321 -3.0642 -0.8682 81 ## 28 20010701 70 18.8 22.7 24.9 5 2 1 0.6840 0.0000 1.3681 67 ## 29 20010702 106 24.1 28.4 30.1 0 0 1 2.8191 3.9392 3.4641 70 ## 30 20010703 139 26.6 30.1 31.9 0 1 4 1.8794 2.0000 1.3681 106 ## 31 20010704 79 19.5 18.8 17.8 8 8 8 0.6946 -0.8660 -1.0261 139 ## 32 20010705 93 16.8 18.2 22.0 8 8 6 0.0000 0.0000 1.2856 79 ## 33 20010706 97 20.8 23.7 25.0 2 3 4 0.0000 1.7101 -2.7362 93 ## 34 20010707 113 17.5 18.2 22.7 8 8 5 -3.7588 -3.9392 -4.6985 97 ## 35 20010708 72 18.1 21.2 23.9 7 6 4 -2.5981 -3.9392 -3.7588 113 ## 36 20010709 88 19.2 22.0 25.2 4 7 4 -1.9696 -3.0642 -4.0000 72 ## 37 20010710 77 19.4 20.7 22.5 7 8 7 -6.5778 -5.6382 -9.0000 88 ## 38 20010711 71 19.2 21.0 22.4 6 4 6 -7.8785 -6.8937 -6.8937 77 ## 39 20010712 56 13.8 17.3 18.5 8 8 6 1.5000 -3.8302 -2.0521 71 ## 40 20010713 45 14.3 14.5 15.2 8 8 8 0.6840 4.0000 2.9544 56 ## 41 20010714 67 15.6 18.6 20.3 5 7 5 -3.2139 -3.7588 -4.0000 45 ## 42 20010715 67 16.9 19.1 19.5 5 5 6 -2.2981 -3.7588 0.0000 67 ## 43 20010716 84 17.4 20.4 21.4 3 4 6 0.0000 0.3473 -2.5981 67 ## 44 20010717 63 15.1 20.5 20.6 8 6 6 2.0000 -5.3623 -6.1284 84 ## 45 20010718 69 15.1 15.6 15.9 8 8 8 -4.5963 -3.8302 -4.3301 63 ## 46 20010719 92 16.7 19.1 19.3 7 6 4 -2.0521 -4.4995 -2.7362 69 ## 47 20010720 88 16.9 20.3 20.7 6 6 5 -2.8191 -3.4641 -3.0000 92 ## 48 20010721 66 18.0 21.6 23.3 8 6 5 -3.0000 -3.5000 -3.2139 88 ## 49 20010722 72 18.6 21.9 23.6 4 7 6 0.8660 -1.9696 -1.0261 66 ## 50 20010723 81 18.8 22.5 23.9 6 3 2 0.5209 -1.0000 -2.0000 72 ## 51 20010724 83 19.0 22.5 24.1 2 4 6 0.0000 -1.0261 0.5209 81 ## 52 20010725 149 19.9 26.9 29.0 3 4 3 1.0000 -0.9397 -0.6428 83 ## 53 20010726 153 23.8 27.7 29.4 1 1 4 0.9397 1.5000 0.0000 149 ## 54 20010727 159 24.0 28.3 26.5 2 2 7 -0.3420 1.2856 -2.0000 153 ## 55 20010728 149 23.3 27.6 28.8 4 6 3 0.8660 -1.5321 -0.1736 159 ## 56 20010729 160 25.0 29.6 31.1 0 3 5 1.5321 -0.6840 2.8191 149 ## 57 20010730 156 24.9 30.5 32.2 0 1 4 -0.5000 -1.8794 -1.2856 160 ## 58 20010731 84 20.5 26.3 27.8 1 0 2 -1.3681 -0.6946 0.0000 156 ## 59 20010801 126 25.3 29.5 31.2 1 4 4 3.0000 3.7588 5.0000 84 ## 60 20010802 116 21.3 23.8 22.1 7 7 8 0.0000 -2.3941 -1.3892 126 ## 61 20010803 77 20.0 18.2 23.6 5 7 6 -3.4641 -2.5981 -3.7588 116 ## 62 20010804 63 18.7 20.6 20.3 6 7 7 -5.0000 -4.9240 -5.6382 77 ## 63 20010805 54 18.6 18.7 17.8 8 8 8 -4.6985 -2.5000 -0.8682 63 ## 64 20010806 65 19.2 23.0 22.7 8 7 7 -3.8302 -4.9240 -5.6382 54 ## 65 20010807 72 19.9 21.6 20.4 7 7 8 -3.0000 -4.5963 -5.1962 65 ## 66 20010808 60 18.7 21.4 21.7 7 7 7 -5.6382 -6.0622 -6.8937 72 ## 67 20010809 70 18.4 17.1 20.5 3 6 3 -5.9088 -3.2139 -4.4995 60 ## 68 20010810 77 17.1 20.0 20.8 4 5 4 -1.9284 -1.0261 0.5209 70 ## 69 20010811 98 17.8 22.8 24.3 1 1 0 0.0000 -1.5321 -1.0000 77 ## 70 20010812 111 20.9 25.2 26.7 1 5 2 -1.0261 -3.0000 -2.2981 98 ## 71 20010813 75 18.8 20.5 26.0 8 7 1 -0.8660 0.0000 0.0000 111 ## 72 20010814 116 23.5 29.8 31.7 1 3 5 1.8794 1.3681 0.6946 75 ## 73 20010815 109 20.8 23.7 26.6 8 5 4 -1.0261 -1.7101 -3.2139 116 ## 74 20010819 67 18.8 21.1 18.9 7 7 8 -5.3623 -5.3623 -2.5000 86 ## 75 20010820 76 17.8 21.3 24.0 7 5 5 -3.0642 -2.2981 -3.9392 67 ## 76 20010821 113 20.6 24.8 27.0 1 1 2 1.3681 0.8682 -2.2981 76 ## 77 20010822 117 21.6 26.9 28.6 6 6 4 1.5321 1.9284 1.9284 113 ## 78 20010823 131 22.7 28.4 30.1 5 3 3 0.1736 -1.9696 -1.9284 117 ## 79 20010824 166 19.8 27.2 30.8 4 0 1 0.6428 -0.8660 0.6840 131 ## 80 20010825 159 25.0 33.5 35.5 1 1 1 1.0000 0.6946 -1.7101 166 ## 81 20010826 100 20.1 22.9 27.6 8 8 6 1.2856 -1.7321 -0.6840 159 ## 82 20010827 114 21.0 26.3 26.4 7 4 5 3.0642 2.8191 1.3681 100 ## 83 20010828 112 21.0 24.4 26.8 1 6 3 4.0000 4.0000 3.7588 114 ## 84 20010829 101 16.9 17.8 20.6 7 7 7 -2.0000 -0.5209 1.8794 112 ## 85 20010830 76 17.5 18.6 18.7 7 7 7 -3.4641 -4.0000 -1.7321 101 ## 86 20010831 59 16.5 20.3 20.3 5 7 6 -4.3301 -5.3623 -4.5000 76 ## 87 20010901 78 17.7 20.2 21.5 5 5 3 0.0000 0.5209 0.0000 59 ## 88 20010902 76 17.3 22.7 24.6 4 5 6 -2.9544 -2.9544 -2.0000 78 ## 89 20010903 55 15.3 16.8 19.2 8 7 5 -1.8794 -1.8794 -2.3941 76 ## 90 20010904 71 15.9 19.2 19.5 7 5 3 -6.1284 0.0000 -1.3892 55 ## 91 20010905 66 16.2 18.9 19.3 2 5 6 -1.3681 -0.8682 1.7101 71 ## 92 20010906 59 18.3 18.3 19.0 7 7 7 -3.9392 -1.9284 -1.7101 66 ## 93 20010907 68 16.9 20.8 22.5 6 5 7 -1.5000 -3.4641 -3.0642 59 ## 94 20010908 63 17.3 19.8 19.4 7 8 8 -4.5963 -6.0622 -4.3301 68 ## 95 20010912 78 14.2 22.2 22.0 5 5 6 -0.8660 -5.0000 -5.0000 62 ## 96 20010913 74 15.8 18.7 19.1 8 7 7 -4.5963 -6.8937 -7.5175 78 ## 97 20010914 71 15.2 17.9 18.6 6 5 1 -1.0419 -1.3681 -1.0419 74 ## 98 20010915 69 17.1 17.7 17.5 6 7 8 -5.1962 -2.7362 -1.0419 71 ## 99 20010916 71 15.4 17.7 16.6 4 5 5 -3.8302 0.0000 1.3892 69 ## 100 20010917 60 13.7 14.0 15.8 4 5 4 0.0000 3.2139 0.0000 71 ## 101 20010918 42 12.7 14.3 14.9 8 7 7 -2.5000 -3.2139 -2.5000 60 ## 102 20010919 65 14.8 16.3 15.9 7 7 7 -4.3301 -6.0622 -5.1962 42 ## 103 20010920 71 15.5 18.0 17.4 7 7 6 -3.9392 -3.0642 0.0000 65 ## 104 20010921 96 11.3 19.4 20.2 3 3 3 -0.1736 3.7588 3.8302 71 ## 105 20010922 98 15.2 19.7 20.3 2 2 2 4.0000 5.0000 4.3301 96 ## 106 20010923 92 14.7 17.6 18.2 1 4 6 5.1962 5.1423 3.5000 98 ## 107 20010924 76 13.3 17.7 17.7 7 7 6 -0.9397 -0.7660 -0.5000 92 ## 108 20010925 84 13.3 17.7 17.8 3 5 6 0.0000 -1.0000 -1.2856 76 ## 109 20010927 77 16.2 20.8 22.1 6 5 5 -0.6946 -2.0000 -1.3681 71 ## 110 20010928 99 16.9 23.0 22.6 6 4 7 1.5000 0.8682 0.8682 77 ## 111 20010929 83 16.9 19.8 22.1 6 5 3 -4.0000 -3.7588 -4.0000 99 ## 112 20010930 70 15.7 18.6 20.7 7 7 7 0.0000 -1.0419 -4.0000 83 ## vent pluie ## 1 Nord Sec ## 2 Nord Sec ## 3 Est Sec ## 4 Nord Sec ## 5 Ouest Sec ## 6 Ouest Pluie ## 7 Ouest Sec ## 8 Nord Sec ## 9 Nord Sec ## 10 Ouest Sec ## 11 Nord Sec ## 12 Sud Sec ## 13 Sud Sec ## 14 Ouest Pluie ## 15 Nord Sec ## 16 Ouest Sec ## 17 Ouest Sec ## 18 Nord Sec ## 19 Est Sec ## 20 Sud Sec ## 21 Nord Sec ## 22 Est Sec ## 23 Sud Sec ## 24 Ouest Sec ## 25 Ouest Pluie ## 26 Sud Sec ## 27 Ouest Sec ## 28 Nord Sec ## 29 Est Sec ## 30 Sud Sec ## 31 Ouest Sec ## 32 Sud Pluie ## 33 Nord Sec ## 34 Ouest Pluie ## 35 Ouest Pluie ## 36 Ouest Sec ## 37 Ouest Sec ## 38 Ouest Sec ## 39 Ouest Pluie ## 40 Est Pluie ## 41 Ouest Pluie ## 42 Ouest Pluie ## 43 Sud Sec ## 44 Ouest Pluie ## 45 Ouest Pluie ## 46 Nord Sec ## 47 Ouest Pluie ## 48 Sud Sec ## 49 Ouest Sec ## 50 Nord Sec ## 51 Nord Sec ## 52 Ouest Sec ## 53 Nord Sec ## 54 Nord Sec ## 55 Ouest Sec ## 56 Sud Sec ## 57 Ouest Sec ## 58 Nord Sec ## 59 Est Sec ## 60 Sud Pluie ## 61 Ouest Pluie ## 62 Ouest Pluie ## 63 Sud Pluie ## 64 Ouest Sec ## 65 Ouest Pluie ## 66 Ouest Pluie ## 67 Nord Pluie ## 68 Nord Sec ## 69 Ouest Pluie ## 70 Ouest Sec ## 71 Nord Sec ## 72 Sud Sec ## 73 Sud Sec ## 74 Ouest Pluie ## 75 Ouest Pluie ## 76 Sud Sec ## 77 Sud Pluie ## 78 Ouest Sec ## 79 Ouest Sec ## 80 Sud Sec ## 81 Ouest Sec ## 82 Est Sec ## 83 Est Sec ## 84 Nord Pluie ## 85 Ouest Sec ## 86 Ouest Pluie ## 87 Nord Pluie ## 88 Ouest Pluie ## 89 Ouest Pluie ## 90 Nord Pluie ## 91 Nord Pluie ## 92 Nord Pluie ## 93 Ouest Pluie ## 94 Ouest Sec ## 95 Ouest Sec ## 96 Ouest Pluie ## 97 Nord Pluie ## 98 Nord Pluie ## 99 Nord Sec ## 100 Nord Pluie ## 101 Nord Pluie ## 102 Ouest Pluie ## 103 Ouest Sec ## 104 Est Pluie ## 105 Est Sec ## 106 Nord Sec ## 107 Ouest Pluie ## 108 Sud Sec ## 109 Sud Pluie ## 110 Sud Sec ## 111 Ouest Pluie ## 112 Sud Sec ``` :Aide{#herexp, toggle=popup, title-display=hidden} Le jeu de données `her` rassemble * des données d'identité (numéro d'indentification, sexe, age) * des caractéristiques du corps humain (poids, taille, pouls, pression systolique, pression diastolique, taux de cholestérol, indice de masse corporel, circonférence de jambe, coude, poignet et bras). Le modèle usuel de régression linéaire multiple est le suivant : $\begin{align*}y &= \beta_0 + \beta_1 x_{1} + \beta_2 x_{2} + \cdots + \beta_p x_{p} + \varepsilon_i\\ &= \beta_0 + \sum_{j=1}^p\beta_j x_{j} + \varepsilon \end{align*}$ où : * $y$ est une variable, quantitative continue, à expliquer (ou variable dépendante), * $x_1, \ldots, x_p$ sont des variables, quantitatives continues, explicatives, * $\varepsilon$ est un terme d'erreur aléatoire de loi normale d'espérance nulle et d'écart-type $\sigma$. Pour réaliser une régression linéaire multiple, la fonction `lm()` est utilisée comme en régression linéaire simple. |Rôle|Commande R| Arguments|Exemple| |----|----|----|----| |Régression linéaire multiple|lm(y~x+z+t...)|[formule](#formula2)|[ici](#reg)| :Aide {#formula2, toggle=popup} L’option formula (la première de la fonction `lm()`) décrit le modèle que l’on souhaite tester, avec la convention que le terme à expliquer $y$ se trouve à gauche du symbole ~. |Rôle|Commande R|Remarque| |---|---|---| |toutes les variables explicatives|y~.|l’ensemble des variables disponibles dans le jeu de données (à l’exception de y bien entendu) vont intervenir dans la partie explicative du modèle| |variables choisies| y~x+z| seules les variables explicatives x et z vont intervenir dans le modèle| :Exemple {#reg, toggle=popup} Le modèle linéaire multiple pour l'exemple `ozone` faisant intervenir toutes les variables explicatives est le suivant : $\begin{align*} \mathtt{maxO3} &= \beta_0 + \beta_1 \mathtt{T9} + \beta_2 \mathtt{T12} + \beta_3 \mathtt{12} + \beta_4 \mathtt{Ne9} + \beta_5 \mathtt{Ne12} + \beta_6 \mathtt{Ne15}+ \\ & \quad + \beta_7 \mathtt{Vx9} + \beta_8 \mathtt{Vx12} + \beta_9 \mathtt{Vx15} + \beta_{10} \mathtt{maxO3v} + \varepsilon \end{align*}$ Pour obtenir les résultats d'estimation du modèle de régression linéaire multiple entre `maxO3` la variable à expliquer et l'ensemble des variables explicatives quantitatives: ```r ozone <- subset(ozone, select = -c(vent, pluie)) regmult <- lm(maxO3 ~ ., data = ozone) ``` Comme en régression linéaire simple, les résultats de la régression s'obtiennent en affichant l'objet de régression et avec la fonction `summary()`. Des informations sur le modèle qui a été estimé sont affichées : estimations, mesures de qualité du modèle... |Rôle|Commande R| Remarque|Exemple| |----|----|----|----| |Résultats basiques|nom_de_la_regression|[Informations contenues dans la régression](#cpltreg)|[ici](#reg2)| |Résultats détailés|summary()|[Compléments sur les résultats de `summary()`](#reg4)|[ici](#reg3)| :Exemple {#reg2, toggle=popup} ```r regmult ``` ``` ## ## Call: ## lm(formula = maxO3 ~ ., data = ozone) ## ## Coefficients: ## (Intercept) X T9 T12 T15 Ne9 ## 2.762e+05 -1.380e-02 -4.259e-01 2.413e+00 7.011e-01 -2.213e+00 ## Ne12 Ne15 Vx9 Vx12 Vx15 maxO3v ## -2.248e-01 2.827e-01 6.900e-01 1.709e-01 5.730e-01 3.458e-01 ``` R renvoie uniquement la commande que l'on a tapée, ainsi que les estimations $(\hat{\beta}_0, \ldots, \hat{\beta}_{i,p}),~i=1,\dots,n\ $ des coefficients $({\beta}_0, \ldots, {\beta}_{i,p}),~i=1,\dots,n\ $ associés aux variables explicatives. Chaque estimation est identifiée par le nom de la variable explicative associée ou par la mention `(intercept)` pour $\hat{\beta}_0 $. :Exemple {#reg3, toggle=popup} ```r summary(regmult) ``` ``` ## ## Call: ## lm(formula = maxO3 ~ ., data = ozone) ## ## Residuals: ## Min 1Q Median 3Q Max ## -53.646 -8.336 0.422 8.167 38.881 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 2.762e+05 2.869e+05 0.963 0.3380 ## X -1.380e-02 1.434e-02 -0.963 0.3380 ## T9 -4.259e-01 1.202e+00 -0.354 0.7239 ## T12 2.413e+00 1.447e+00 1.667 0.0986 . ## T15 7.011e-01 1.155e+00 0.607 0.5451 ## Ne9 -2.213e+00 9.389e-01 -2.357 0.0204 * ## Ne12 -2.248e-01 1.383e+00 -0.162 0.8713 ## Ne15 2.827e-01 1.008e+00 0.280 0.7798 ## Vx9 6.900e-01 9.511e-01 0.726 0.4698 ## Vx12 1.709e-01 1.066e+00 0.160 0.8729 ## Vx15 5.730e-01 9.299e-01 0.616 0.5392 ## maxO3v 3.458e-01 6.324e-02 5.468 3.35e-07 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 14.37 on 100 degrees of freedom ## Multiple R-squared: 0.766, Adjusted R-squared: 0.7403 ## F-statistic: 29.76 on 11 and 100 DF, p-value: < 2.2e-16 ``` Pour les données ozone, le modèle estimé présente une bonne qualité d’adéquation aux données. Cependant, plusieurs variables explicatives ne semblent pas utiles dans ce modèle. :Compléments {#cpltreg, toggle=popup, title-dispay=hidden} L'objet `régression linéaire` est en réalité une liste contenant un grand nombre d'informations (on y accède grâce au `$`) comme par exemple : * `coefficients` qui contient le vecteur des estimations des coefficients, * `fitted.values` qui contient les valeurs ajustées $\hat{y}_i =\hat{\beta}_0 + \hat{\beta}_1 x_i$, pour $i$ allant de $1$ à $n$, * `residuals` qui contient les résidus $e_i = y_i - \hat{y}_i$, pour $i$ allant de $1$ à $n$ :Compléments sur les résultats de `summary()`{#reg4, toggle=popup} Les informations données par la fonction `summary()` concernent : * les résidus (maximum, minimum, quartiles), * les coefficients : en plus des estimations des $\beta_j$ (`Estimate`), l'écart-type estimé des estimateurs correspondants (`Std. Error`) est donné, ainsi que la valeur de la statistique de test (`t value`) et la p-value (`Pr(>|t|)`) associées aux tests de Student ($H_0 : \beta_j = 0$ contre $H_1 : \beta_j \neq 0$) correspondants. A noter que des étoiles pour chaque coefficient indiquent le niveau de significativité des différents tests. * la qualité d'adéquation du modèle : une estimation de $\sigma$, l'écart-type du terme d'erreur (`Residual standard error`), la valeur du $R^2$ (`Multiple R-squared`) et celle du $R^2$ ajusté (`Adjusted R-squared`), et enfin la valeur de la statistique de test (`F-statistic`) et la p-value du test de Fisher de significativité du modèle ($H_0 : \beta_1 = \ldots = \beta_p = 0$ contre $H_1$ : au moins un $\beta_j \neq 0$). Ce dernier test permet de tester la nullité simultanée de tous les coefficients associés aux variables explicatives. Ainsi accepter $H_0$ signifie que le modèle proposé n'est pas adéquat. :Remarque concernant le $R^2$ ajusté {#adjRsqua, toggle=collapse} Le $R^2$ ajusté présente un intérêt uniquement dans le cas où plusieurs modèles ajustés sur un même jeu de données sont comparés. En effet, il s'agit d'une version du $R^2$ pénalisée par le nombre de variables explicatives. Le meilleur modèle est celui qui possède la plus grande valeur du $R^2$ ajusté. De même que pour la régression linéaire simple, il est possible de faire des graphiques (ou des tests) pour vérifier les hypothèses du modèle de manière visuelle, et aussi de tester la normalité des résidus. Les deux hypothèses à tester sont donc : * L'homogénéité de la variance (homoscédasticité) * La normalité des résidus. |Rôle | Commande R | Remarque|Exemple| |---------|--------|---------|--------| |Graphique des valeurs prédites | `plot()` / `abline()` |adéquation prédiction / mesure | [ici](#ex_fitted_ozone) | |Graphique des résidus | `plot()` |hypothèse variance homogène| [ici](#ex_resid_ozone) | |Histogramme des résidus | `hist()` / `curve()` |hypothèse normalité des résidus| [ici](#ex_hist_resid_ozone) | |Graphique quantile par quantile | `qqnorm()` | hypothèse normalité des résidus| [ici](#ex_qq_ozone) | |Test de normalité des résidus | `shapiro.test()` |hypothèse normalité des résidus| [ici](#ex_shapiro_ozone) | :Exemple {#ex_resid_ozone, toggle=popup} ```r plot(regmult$fitted.values, regmult$residuals) abline(h = 0, col = "darkgreen", lwd = 2) ```  Aucun schéma particulier ne se dégage du graphique signe d'une variance homogène. :Exemple {#ex_fitted_ozone, toggle=popup} ```r plot(ozone$maxO3, regmult$fitted.values) abline(a = 0, b = 1, col = "blue", lwd = 2) ```  Les valeurs prédites par le modèle sont proches des valeurs utilisées pour construire ce dernier (les points sont proches de la première bissectrice), le modèle est donc adapté. :Exemple {#ex_hist_resid_ozone, toggle=popup} Dans le modèle linéaire, la normalité du terme d'erreur aléatoire $\varepsilon$ est supposée. Il faut vérifier cette hypothèse, qui est très importante. Dans un premier temps, une vérification graphique peut être faite, en traçant l'histogramme des résidus. De plus, la courbe représentative de la densité de la loi normale de paramètres $0$ et l'écart-type estimé des résidus peut être superposée. ```r histo <- hist(regmult$residuals, probability = TRUE) ec_typ <- summary(regmult)$sigma curve(dnorm(x, 0, ec_typ), from = min(histo$breaks), to = max(histo$breaks), add = TRUE, type = "l", col = "magenta", lwd = 2) ```  :Exemple {#ex_qq_ozone, toggle=popup} ```r ec_typ <- summary(regmult)$sigma normed_res <- regmult$residuals/ec_typ qqnorm(normed_res, xlim = range(normed_res), ylim = range(normed_res)) abline(0, 1, col = "cadetblue", lwd = 2) ```  Le qqplot des résidus re-normalisés doit être relativement proche de la première bissectrice pour valider graphiquement l'hypothèse de normalité. :Exemple {#ex_shapiro_ozone, toggle=popup} ```r shapiro.test(regmult$residuals) ``` ``` ## ## Shapiro-Wilk normality test ## ## data: regmult$residuals ## W = 0.96902, p-value = 0.01049 ``` La p-value, de 0.01, est inférieure à 5%, donc on rejette l'hypothèse de normalité des résidus. :Remarque {#plotreg, toggle=collapse} Les graphiques des résidus et quantile-quantile peuvent être obtenus directement à partir de la commande `plot(regression)`. ```r par(mfrow=c(2,2)) plot(regmult) ``` 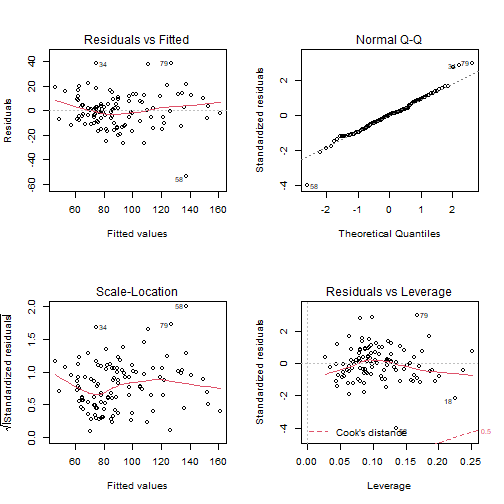 Cette fonction renvoie quatre graphiques (de gauche à droite et de haut en bas) : * Le graphique des résidus (`Residuals vs Fitted`) * Le graphique quantile-quantile (`Normal Q-Q`) * Le graphique de `scale location` : similaire au graphique des résidus où aucun schéma ne doit se distinguer pour pouvoir valider le modèle; * Le `Residuals vs Leverage`. Ce graphique représente « le poids » de chaque expérience dans la régression. Les points éloignés du centroïde (point 0,0) ont une forte incidence sur la régression et leur suppression conduirait à largement modifier cette dernière. Ainsi les points situés au-delà des courbes en pointillé rouge sont des points à considérer car ils influent beaucoup sur la détermination du modèle. Ici, c'est l'effet de levier qui est mis en évidence. :Remarque par(mfrow=c(2,2)) {#rmqpar, toggle=collapse} Cette commande sert à scinder la fenêtre graphique en deux lignes et deux colonnes pour afficher les quatre graphiques simultanément. :Suite Régression linéaire multiple {#regmul, toggle=collapse, title-display=hidden} [Approche descriptive préliminaire](caps_9_1_regression_lineaire_multiple_description.html) [Mise en oeuvre](caps_9_2_regression_lineaire_multiple_mise_en_oeuvre.html) [Affiner le modèle](caps_9_3_regression_lineaire_multiple_affiner.html)