Begin'R
Les statistiques avec R
Navigation
[Retour au sommaire]
# Description de variables quantitatives :Objectifs Représenter graphiquement des variables quantitatives à l'aide d'un histogramme ou d'une boîte à moustaches. Les exemples de la suite sont tirés du [jeu de données Melons](caps_2_1_presentation_donnees_melons.html). | Rôle | Commande R |Remarques |Exercice | |---------------------|-----------------|----------------------|--------------------------| |Histogramme |`hist()` | [ ici ](#hist) | [ ici ](#exo_hist) | |Boîtes à moustaches |`boxplot()` | [ ici ](#boxplot) | [ ici ](#exo_boxplot) | :Remarque {#hist, toggle=popup} Sous R, la fonction **`hist()`** permet de réaliser, de manière totalement automatique, **un histogramme**. Pour cela, elle gère de façon transparente les trois aspects suivants : + la définition des classes (le nombre de classes est déterminé par la règle de _Sturges_, les bornes des classes sont ajustées au mieux), + le dénombrement des individus, classe par classe, + le tracé des effectifs des classes sous la forme d'un histogramme. :Exemple {#hist-poids} Réalisons l'histogramme de la variable `Poids` du jeu de données sur les melons. ```r hist(melons$Poids) ```  On peut rajouter de la couleur (argument `col`) et un titre (argument `main`). ```r hist(melons$Poids, main="Histogramme du poids moyen des melons", col="pink") ```  Si nécessaire, il est possible de modifier le nombre de classes avec l'argument `breaks` : + `breaks=10` permettrait par exemple de fixer le nombre de classes à 10, + `breaks="FD"` permettrait de déterminer le nombre de classes selon la règle de Freedman-Diaconis, +`breaks="Scott"` permettrait de déterminer le nombre de classes selon la règle de Scott, + `breaks=seq(600,1400,200)` conduirait à des classes de largeur constante égale à 200, entre 600 et 1400. :Exercice{#exo_hist, toggle=popup} Réaliser trois histogrammes pour le poids des melons en choisissant, grâce à l'argument `breaks`, respectivement : + 5 classes + 32 classes entre 600 et 1400, + un nombre de classes choisi selon la règle de Scott, On affichera les **fréquences relatives** et non les fréquences absolues (effectifs). :Corrigé{#answer_histo, toggle=collapse, title-display=show} ```r hist(melons$Poids, freq=FALSE, breaks=5) ``` 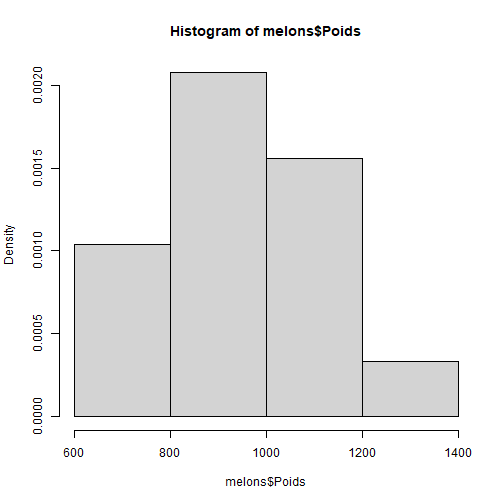 Le nombre de classes est ici trop faible et conduit à une simplification extrême de la forme de l'histogramme. On constate en passant que la fonction `hist` a constitué 4 et non 5 classes, contrairement à ce qui a été demandé. En réalité, la fonction ajuste automatiquement le nombre de classes de façon à obtenir des limites de classes pertinentes (ici, des multiples de 200)). ```r hist(melons$Poids, freq=FALSE, breaks=seq(600,1400,25)) ``` 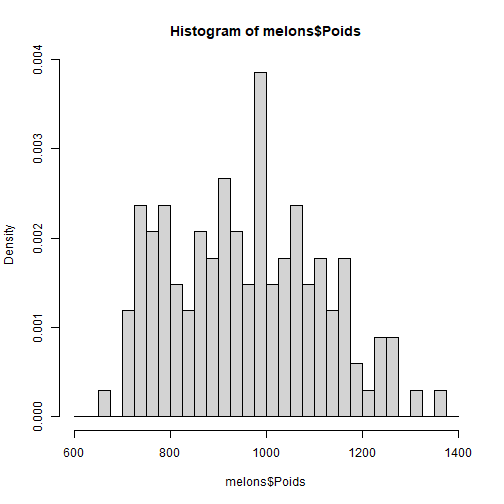 Dans ce nouveau graphique, au contraire, les classes sont trop nombreuses. L'histogramme montre ici trop de détails, ce qui est inutile et contre-productif pour réaliser un résumé synthétique et efficace de la série de données. ```r hist(melons$Poids, freq=FALSE, breaks="Scott") ```  Le nombre de classes déterminé par la règle de Scott est en réalité le même que celui déterminé par celle de Sturges (méthode par défaut). C'est un bon compromis qui préserve un caractère synthétique tout en permettant d'appréhender la forme de la distribution. On voit ici aussi que les limites de classes sont calées sur des multiples de 100. :Remarque{#boxplot, toggle=popup} Pour obtenir une boîte à moustaches, il suffit d'utiliser la fonction **`boxplot()`** avec comme argument la variable considérée. :Exemple {#boitepoids} La boîte à moustaches du poids des melons est la suivante : ```r boxplot(melons$Poids) ```  On peut rajouter de la couleur avec l'argument `col`. ```r boxplot(melons$Poids, col="grey") ```  :Exercice{#exo_boxplot, toggle=popup} Réaliser la boîte à moustaches de la variable rendement (`Rdt`) de la base de données `melons`. :Corrigé{#answer_boxplot, toggle=collapse, title-display=show} ```r boxplot(melons$Rdt, col="cadetblue") ```  Les valeurs jugées extrêmes (dépassant de la patte inférieure) ont été représentées à l'aide de ronds. :Compléments : Détection des valeurs aberrantes{#pourallerplusloin2, toggle=collapse, title-display=show} Lorsque des valeurs extrêmes (_outliers_ en anglais), pouvant être considérées suspectes ou aberrantes, existent dans une série de données, la fonction `boxplot()` les représente par des ronds au-delà des pattes supérieure et inférieure. Toutefois, R n'indique pas quelles sont ces valeurs et il peut être utile de les identifier. Pour obtenir ces informations, il suffit de stocker le résultat de `boxplot()`dans un objet nommé `b` par exemple, et d'utiliser `b$stats` qui renvoie successivement le minimum, le premier quartile, la médiane, le troisième quartile et le maximum. On obtient alors : - `min`, le minimum de la variable considérée en tapant `min = b$stats[1]` - `Q1`, le premier quartile avec `Q1 = b$stats[2]` - `Q2`, la médiane avec `Q2 = b$stats[3]` - `Q3`, le troisième quartile avec `Q3 = b$stats[4]` - `max`, le maximum avec `max = b$stats[5]` - l'intervalle interquartile avec `IQR = Q3 - Q1` - la limite basse avec `limite_basse = Q1 - 1.5*IQR` - la limite haute : `limite_haute = Q3 + 1.5*IQR` - les observations qui correspondent à des valeurs aberrantes dans la queue basse de la distribution avec `outliersbas = which(nom_variable < limite_basse)` - les observations qui correspondent à des valeurs aberrantes dans la queue haute de la distribution avec `outliershauts = which(nom_variable > limite_haute)` [ Exemple ici ](#exemple_outliers) :Exemple{#exemple_outliers, toggle=popup} Voici les instructions permettant de déterminer les valeurs aberrantes dans la variable rendement. ```r b = boxplot(melons$Rdt) ``` 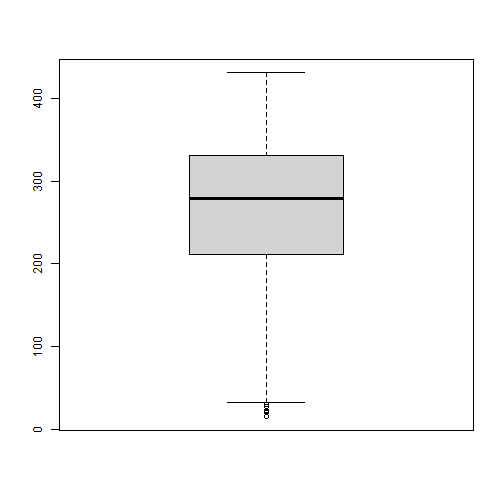 ```r IQR=b$stats[4]-b$stats[2] limite_basse=b$stats[2]-1.5*IQR limite_haute=b$stats[4]+1.5*IQR outliers_bas=which(melons$Rdt < limite_basse) outliers_bas ``` ``` ## [1] 21 35 36 52 70 84 86 87 129 ``` ```r length(outliers_bas) ``` ``` ## [1] 9 ``` ```r outliers_hauts=which(melons$Rdt > limite_haute) length(outliers_hauts) ``` ``` ## [1] 0 ``` Il y a 9 observations dans la base de données (R vous donne leur numéro) qui correspondent à des valeurs aberrantes dans la queue basse de la distribution de la variable rendement. Il n'y en a aucune dans la queue haute. :Suite Statistiques descriptives univariées {#univ, toggle=collapse, title-display=hidden} [Description des variables](caps_uni_1_descriptif.html) [Description de variables qualitatives](caps_uni_quali_1.html) [Représentation de variables qualitatives](caps_uni_quali_2.html) [Description paramètrique de variables quantitatives](caps_uni_3_quanti_1.html)